Hey Russ.
When you responded to my last post, you forgot to address this part:
Stop it!
You are trying to set up the same false claim about the second law of thermodynamics that got you into trouble before.

You are jumping the shark by switching to
machines.

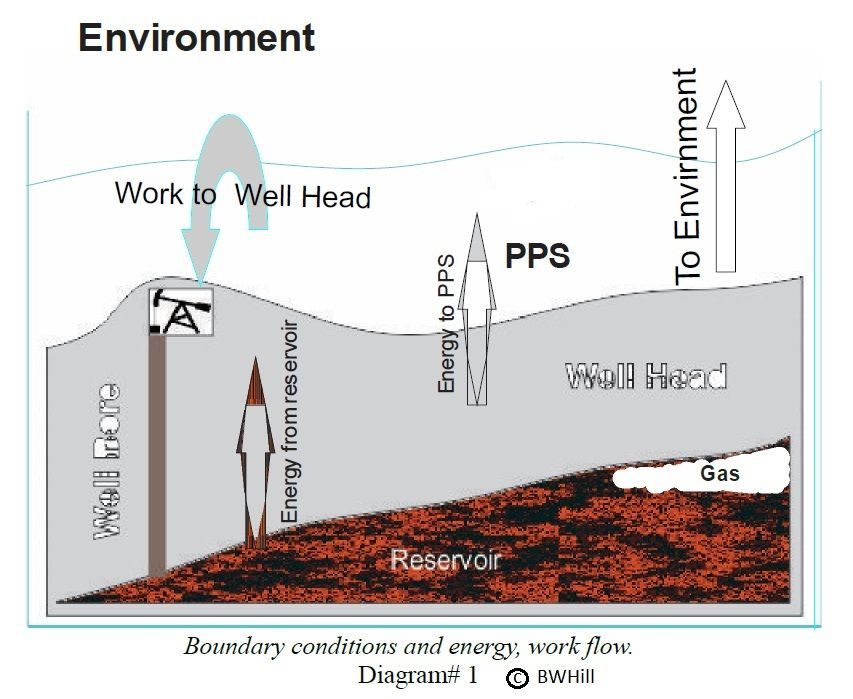
Machines are not relevant because the world oil production system is not a machine! Machines are idealized thermodynamic systems. They are closed systems.
The oil production system is an open system. It can be modeled using the
Entropy Rate Balance Equation for Control Volumes, as is accomplished in the Etp model.
The idealized closed system you keep bringing up so deceptively is what is called adiabatic. Adiabatic means it occurs without transfer of heat or matter between a system and its surroundings; energy is transferred only as work. Closed systems are what is called
reversible. Theoretically their entropy production rate is zero (ΔS = 0), but this does not actually happen in nature.
With the exception of
idealized adiabatic and isentropic systems, all other systems in the universe are open systems. Open systems are what is called
irreversible. That means that their entropy production rate is greater than zero (ΔS > 0).
These are the most basic concepts in thermodynamics, Russ!

You can't just lie about them!
Reread carefully what INFO-MAN and Chestermiller had to say about the subject:
INFO-MAN said:
I agree that most people have a very hard time grasping entropy and the second law of thermodynamics. But I am not sure I understand why your article keeps referring to reversible processes and adiabatic idealizations. In natural systems, the entropy production rate of every process is always positive (ΔS > 0) or zero (ΔS = 0). But only idealized adiabatic (perfectly insulated) and isentropic (frictionless, non-viscous, pressure-volume work only) processes actually have an entropy production rate of zero. Heat is produced, but not entropy. In nature, this ideal can only be an approximation, because it requires an infinite amount of time and no dissipation.
Chestermiller said:
This is an example of one of those instances I was referring to in which the constraints on the equations is not spelled out clearly enough, and, as a result, confusion can ensue.
The situation you are referring to here with the inequality (ΔS > 0) and equality (ΔS = 0) applies to the combination of the system and the surroundings, and not just to a closed system. Without this qualification, the student might get the idea that for a closed system, ΔS≥0 always, which is, of course, not the case.
Even though
reversible processes are an idealization, there is still a need for beginners to understand them...
INFO-MAN said:
You hardly mention irreversible processes. An irreversible process degrades the performance of a thermodynamic system, and results in entropy production. Thus, irreversible processes have an entropy production rate greater than zero (ΔS > 0), and that is really what the second law is all about (beyond the second law analysis of machines or devices). Every naturally occurring process, whether adiabatic or not, is irreversible (ΔS > 0), since friction and viscosity are always present.
Chestermiller said:
I'm sorry that impression came through to you because that was not my intention. I feel that it is very important for students to understand the distinction between real irreversible processes paths and ideal reversible process paths.
Irreversible process paths are what really happens. But reversible process paths are what we need to use to get the change in entropy for a real irreversible process path.
INFO-MAN said:
Here is my favorite example of an irreversible thermodynamic process, the
Entropy Rate Balance Equation for Control Volumes:
$$\frac{dS_{CV}}{dt} =\sum_j\frac{\dot{Q}_{j}}{T_{j}} +\sum_i\dot{m}_{i}s_{i} -\sum_e\dot{m}_{e}s_{e}$$
Chestermiller said:
This equation applies to the more general case of an open system for which mass is entering and exiting, and I was trying to keep things simple by restricting the discussion to closed systems. Also, entropy generation can be learned by the struggling students at a later stage.
INFO-MAN said:
And here are are a couple of other important things you did not mention about entropy:
1) Entropy is a measure of molecular disorder in a system. According to Kelvin, a pure substance at absolute zero temperature is in perfect order, and its entropy is zero. This is the less commonly known Third Law of Thermodynamics.
2) "A system will select the path or assemblage of paths out of available paths that minimizes the potential or maximizes the entropy at the fastest rate given the constraints." This is known as the Law of Maximum Entropy Production. "The Law of Maximum Entropy Production thus has deep implications for evolutionary theory, culture theory, macroeconomics, human globalization, and more generally

 .
. But the number will assuredly be orders of magnitude lower than the enthalpy of burning oil, which means you have proved my point, that the entropy increase mentioned in these equations has negligible impact on our thermodynamic ability to extract the oil, using - as we do - the energy from burning it to help us do so. Anybody with rudimentary understanding of thermodynamics would have realised this at the outset
But the number will assuredly be orders of magnitude lower than the enthalpy of burning oil, which means you have proved my point, that the entropy increase mentioned in these equations has negligible impact on our thermodynamic ability to extract the oil, using - as we do - the energy from burning it to help us do so. Anybody with rudimentary understanding of thermodynamics would have realised this at the outset