The time coordinate has a very specific meaning in this context for observers.
Really? What meaning?
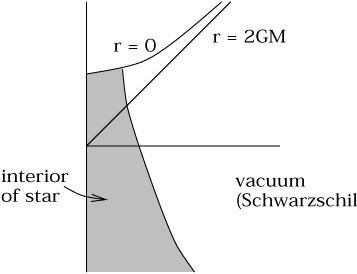
Incidentally, for a spherically symmetric collapsing star, the event horizon also starts at a finite value of the
t coordinate even in a Schwarzschild-like coordinate system. This is not a feature of just Kruskal-like coordinates.
You cannot replace t and r with U and V and then apply the original definitions to the new variables
I didn't. I'm only drawing on two facts: 1) the event horizon forms at a finite value of the timelike (
v) coordinate, and 2) in the Kruskal-like coordinates, the metric is finite everywhere except the singularity (i.e. there are no coordinate singularities), so finite distances on the diagram correspond to e.g. finite space-time intervals.
If you're going to say that the event horizon forms at "negative infinity", the burden of proof is really on you to explain where you're getting that from and to explain why it is a physical result and not an artefact of some coordinate system or other.
(which were derived to accommodate the math, not to describe reality).
You say that as if Schwarzschild-like coordinates
did "describe reality" in some way that Kruskal-like coordinates don't. You shouldn't presume that. In general you shouldn't presume any coordinate system has any special significance except what you can explicitly justify from the metric. For the Schwarzschild black hole solution, Kruskal coordinates have the mathematical convenience that the metric is conformally flat in the
v and
u coordinates, so (the radial sections of) light cones look the same way on a Kruskal diagram as they do on a Minkowski diagram, which makes them convenient for answering questions related to causal relations and structure. Schwarzschild coordinates are defined differently and are more convenient in different respects, the most notable one being that the Schwarzschild metric is static in the Schwarzschild
t coordinate (so for example for two objects at different but constant Schwarzchild radii, the metric components are related in a simple way to the Doppler shifts between them).
Specifically, restricting ourselves to the "region 1" (exterior), where
$$V^2 - U^2 < 0$$ and $$U > 0$$
the transformation between Schwarzschild t and Kruskal U, V is
$$tanh({{t}\over{4GM}}) = V/U$$
U has a lower bound of zero because that is simply what defines region 1; however, V can be negative, which is why $$-\infty <= t <= +\infty$$ for the exterior of any black hole.
You are copying what Wikipedia says about the Schwarzschild
eternal black hole solution and naively applying it to a black hole that has formed by stellar collapse. In this and my previous post, there is a reason I've been referring to "Schwarzschild-like" and "Kruskal-like" coordinates rather than just "Schwarzshild" and "Kruskal" coordinates. The reason is that the latter are really defined in terms of the Schwarzschild
eternal black hole metric taking a particular form in terms of those coordinates. For a black hole forming by stellar collapse, the spacetime metric takes the form of the Schwarzschild metric only
outside the outer surface of the star, and it is
only outside that region that you really have Schwarzchild and Kruskal coordinates that have the same significance and which are related in the same way as in the eternal black hole solution. In particular, inside the star, the Kruskal-like coordinates used in the diagram I gave in post #102 are
not defined by the equations given
here.
In fact, in any region of weak spacetime curvature, such as in and around a star before its gravitational collapse like in the bottom part of the diagram in post #102, Kruskal-like and Schwarzschild-like coordinates are very nearly the same thing. In flat (Minkowski) spacetime, they are
identical.
This may be valid if two events were space-like separated and determining which event occurred first were a matter of perspective, but that is not the case with black hole creation and/or growth: there is not a frame in which the creation occurred "after" negative infinity.
I just gave you one! Even the stellar collapse solution in Schwarzchild-like coordinates has the event horizon forming at some finite
t coordinate.
If you mean something different by "frame" than just "coordinate system", please define what you mean by that.