This definition doesn't support you. It's equivalent to the more familiar definition which says that a black hole is the region of spacetime from which you cannot escape from the singularity. Think about it. If you have an event X in spacetime that is in the past light cone of "future infinity", this means that there's a timelike curve passing via event X that can get to "future infinity", successfully avoiding the singularity. Or, stated differently, X is not in the black hole, because an observer starting at X could escape the singularity. Conversely, if an event Y is
not in the past light cone of "future infinity", then
no timelike curve passing via event Y can reach "future infinity", so (barring really esoteric situations like closed timelike loops) the only alternative for any timelike curve passing via Y is to terminate on a singularity.
An implication of this that I've already told you about is that a black hole can never overlap with an outside observer's causal
past (in fact, it's probably the simplest way to
define what it means to be outside a black hole). This has nothing, logically, to do with whether a black hole can overlap with an outside observer's causal
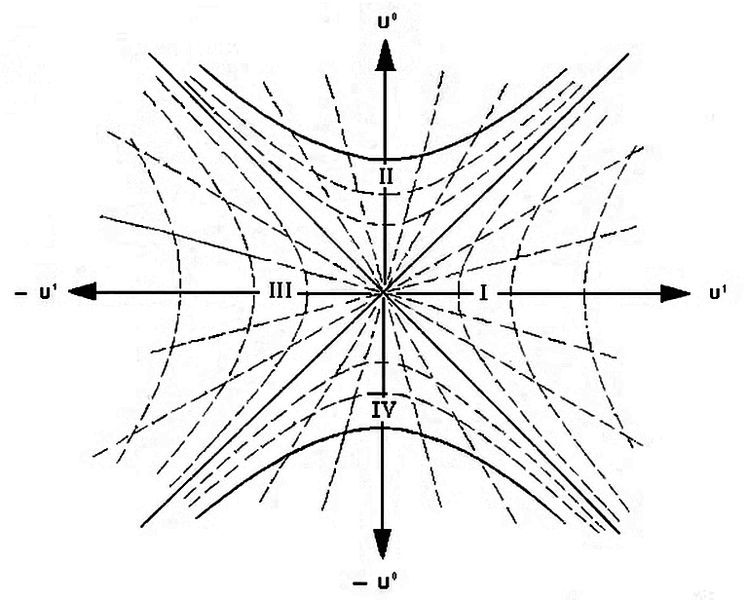
present. The Kruskal chart quite clearly depicts both, for instance. Penrose diagrams depict this even more explicitly.
We don't need to redefine anything at all. You're presuming that we first have to predict the black hole in Schwarzschild coordinates before we can transform to Kruskal coordinates. We don't. The black hole metric expressed in Kruskal coordinates describes a perfectly valid pseudo-Riemannian manifold that can be shown to be a vacuum solution to the Einstein field equation. It is, therefore, a perfectly valid prediction made by general relativity. It is no more than a matter for our history books that the black hole was first derived in Schwarzschild coordinates. There's no fundamental reason it couldn't have happened in the opposite order. So if there really were something fundamentally wrong with Kruskal coordinates and the Kruskal metric expression, you should really be able to point it out
without having to make any reference to Schwarzschild coordinates.
No. Schwarzschild coordinates are defined to have certain "nice" properties. Specifically, the black hole metric is static (time-independent) and spherically symmetric when expressed in Schwarzschild coordinates, asymptotically approaches the Euclidean metric in spherical coordinates in the limit $$r \,\to\, \infty$$, and the locus of points at fixed Schwarzschild radius $$r$$ at any given Schwarzschild time $$t$$ constitutes a surface of area $$4 \pi r^{2}$$. Kruskal coordinates are defined to have different "nice" properties. Specifically, their defining property is that radial null geodesics (light-like curves) always have a coordinate velocity of $$\pm 1$$.
The point is,
both these coordinate systems are, first and foremost, defined
mathematically. That's not to say they can't have any "physical significance", but that's not how they're defined, and if either
does have "physical meaning" it's 1) a bonus and 2) only to the extent it can be justified from its mathematical definition and the corresponding metric expression.
Both coordinate systems have their strengths and weaknesses that follow from their basic properties. For instance, the fact that the metric is static in Schwarzschild coordinates means that you can easily read off certain things (like relative Doppler shifts between observers at constant Schwarzschild radii) more or less directly from the Schwarzschild metric expression. The way the Kruskal chart is defined makes it particularly easy to see the causal structure of the entire black hole manifold.
Neither of these coordinate systems is completely general, by the way, and it's only because the Schwarzschild black hole happens to be quite simple that we can even use these charts at all. If anything, if I'm to believe what I read on Wikipedia (specifically
here), it's actually the
Kruskal construction that is the more general of the two, since it seems that one can always find a conformally flat (i.e. "Kruskal-like") coordinate chart for at least two of the four spacetime dimensions. By contrast, most possible spacetime manifolds are not static or spherically symmetric, and therefore simply wouldn't admit a Schwarzschild-like parameterisation at all.