it is also dated from 2013
The Etp Model Has Been Empirically Confirmed
- Thread starter Futilitist
- Start date
- Status
exchemist
Valued Senior Member
Here is a description of the boundary conditions used in the Etp model and the derivation of equation#7 from the Entropy Rate Balance Equation for Control Volumes:
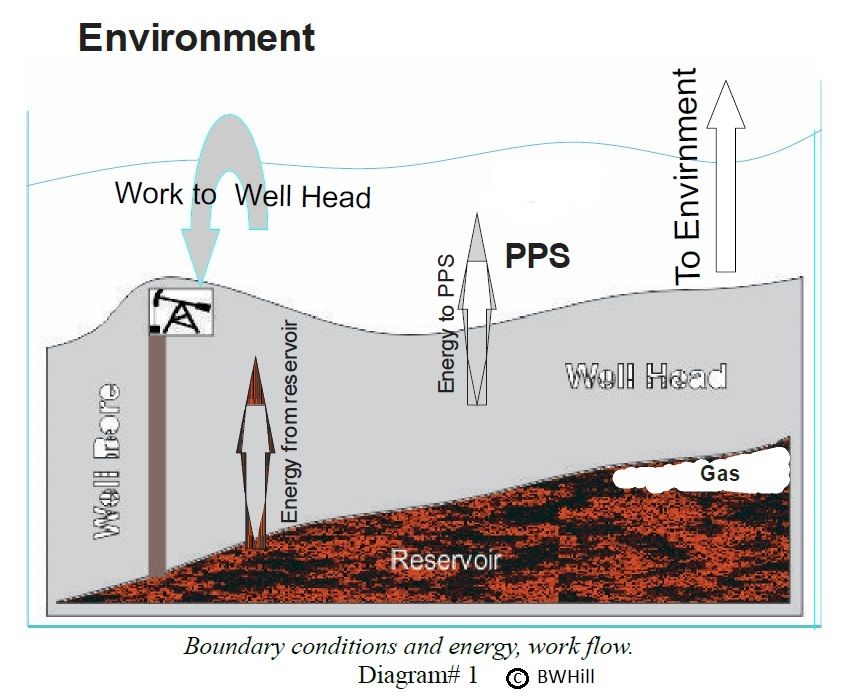
"Crude oil is used primarily as an energy source; its other uses have only minor commercial value. To be an energy source it must therefore be capable of delivering sufficient energy to support its own production process (extraction, processing and distribution); otherwise it would become an energy sink, as opposed to a source. The Total Production Energy ($$E_{TP}$$) must therefore be equal to, or less than EG, its specific exergy. To determine values for $$E_{TP}$$ the total crude oil production system is analyzed by defining it as three nested Control Volumes within the environment. The three Control Volumes (where a control volume differs from a closed system because it allows energy and mass to pass through it's boundaries) are the reservoir, the well head, and the Petroleum Production System (PPS). The PPS is where the energy that comes from the well head is converted into the work required to extract the oil. The PPS is an area which is distributed within, and throughout the environment. It is where the goods and services needed for the production process originate. This boundary make-up allows other energy, and mass transfers to be considered as exchanges, such as natural gas used in refining, electricity used in well pumping, or water used for reservoir injection."
~BW Hill
Values for $$E_{TP}$$ are derived from the solution of the Second Law statement, the Entropy Rate Balance Equation for Control Volumes:
$$\frac{dS_{CV}}{dt}
=\sum_j\frac{\dot{Q}_{j}}{T_{j}}
+\sum_i\dot{m}_{i}s_{i}
-\sum_e\dot{m}_{e}s_{e}
+\dot{\sigma}_{cv}$$
"Where $$\frac{dS_{CV}}{dt}$$ represents the time rate of change of entropy within the control volume. The terms $$\dot{m}_{i}s_{i}$$ and $$\dot{m}_{e}s_{e}$$ account, respectively, for rates of entropy transfer into and out of the control volume accompanying mass flow. The term $$\dot{Q}_{j}$$ represents the time rate of heat transfer at the location on the boundary where the instantaneous temperature is $$T_{j}$$. The ratio $$\frac{\dot{Q}_j}{T_j}$$ accounts for the accompanying rate of entropy transfer. The term $$\dot{\sigma}_{cv}$$ denotes the time rate of entropy production due to irreversibilities within the control volume."
~(Taken from Fundamentals of Engineering Thermodynamics by Moran and Shapiro)
Because there is only one temperature boundary (at the exit point of the reservoir) and no crude oil enters the reservoir from the environment, the equation reduces to:
$$\frac{dS_{CV}}{dt}=\frac{\dot{Q}_{j}}{T_{j}}-\dot{m}_{e}s_{e}+\dot{\sigma}_{cv}$$
giving: $$\frac{BTU}{sec*°R}$$
For this application, crude oil and water can be treated as incompressible substances. Their specific entropies are only affected by a temperature change.
For specific heats: $$c_{v}=c_{p}=c$$, and $$s_{2}-s_{1}=c*\ln{\frac{T_{2}}{T_{1}}}$$ The reservoir temperature is constant, therefore the entropy of the reservoir must decrease at the same rate that the entropy is transferred from the reservoir by mass flow. Thus, the heat leaving the reservoir is negative in sign and the equation becomes:
$$\frac{\dot{Q}_{j}}{T_{j}}=\dot{\sigma}_{cv}$$
giving: $$\frac{BTU}{sec*°R}$$
The rate of entropy production in the petroleum production system is equal to the rate of heat extracted from the reservoir divided by the reservoir temperature.
The rate of irreversibility production in the petroleum production system therefore becomes:
$$\dot{I_{cv}}=T_{O}*\dot\sigma_{cv}$$
giving: $$\frac{BTU}{sec}$$
Where $$T_{O}$$ equals the standard reference temperature of the environment, 537 °R (77° F).
Therefore:
$$E_{TP}=\int_{t1}^{t2}\dot{I_{cv}}dt$$
giving: $$BTU$$
Because the mass removed from the reservoir is limited to crude oil and water, the increase in $$E_{TP}$$ per billion barrels (Gb) of crude extracted as $$ds=c\frac{dT}{T}$$ is:
(Equation#7)
$$\frac{E_{TP/lb}}{Gb}
=\begin{bmatrix}\frac{(m_{c}*c_{c}
+m_{w}*c_{w})(T_{R}-T_{O})}{m_{c}} \end{bmatrix}/Gb$$
giving: BTU/lb/Gb
$$m_{c}$$ = mass of crude, lbs.
$$c_{c}$$ = specific heat of crude, BTU/lb °R
$$m_{w}$$ = mass of water, lbs.
$$c_{w}$$ = specific heat of water, BTU/lb °R
$$T_{R}$$ = reserve temperature, °R
$$T_{O}$$ = standard reference temperature of the environment, 537 °R
$$s_{i}$$ = specific entropy into the control volume
$$s_{e}$$ = specific entropy exiting the control volume
BTU/gal/Gb for 35.7° API crude = BTU/lb/Gb * 7.0479 lb/gal
Evaluation of $$E_{TP}$$ from Equation# 7 requires the determination of three variables: mass of the crude ($$m_{c}$$) mass of the water ($$m_{w}$$), and the temperature of the reservoir ($$T_{R}$$). These must be determined at time (t).
1) The mass of crude at time (t) is derived from the cumulative production function,
2) the mass of water is derived from the average % surface water cut (fw) of the reservoir,
3) temperature of the reserve is derived from the well depth. This assumes an earth temperature gradient of 1°F increase per 70 feet of depth.
-------------------------------
What exactly do you find wrong with the methodology, above, used to develop the Etp function?
---Futilitist
I have told you many times Fute, and any normal person would not need to ask, as it was the subject of the very post to which you are replying!
However, since we now have some moderator attention on the thread I'll do so one last time:-
Where does the energy content of the oil being produced appear in what you have cut and pasted here? Russ and I have looked for this without success.
Without considering this, any pretence that this model can predict the energy available from the production process is entirely empty.
Last edited:
well then, answer this question below so i cannot " misinterpret "(ahh yes-yes-- there is that word that is used when individuals do not comprehend the words they have read) since i agree with origin:
" after 76 pages of this, i still do not have a clue as to what this etp model actually predicts. from what i can gather is that it predicts a range--which strangely enough is from 11 dollars to 66 dollars--which will then cause society to collapse-- am i now understanding this? "
That is because what you are looking for is not there. It is not necessary to evaluate the energy content of the oil being produced. The energy content of a barrel of oil never changes. It is the same as it has always been. What changes is the amount of energy required to produce the next barrel. That rises because of rising entropy production in the petroleum processing system. The Etp model measures rising entropy by using the Entropy Rate Balance Equation for Control Volumes, which is a second law statement.
No.
---Futilitist
Last edited:
when i tried to " interpret "(since it is not an actual phrase) the phrase, all i revived was nothing but food data--strange-- are you making shiit up ?
the next sentence that you conveniently left-out states why(and you are whining about word games, correct?).
Then why doesn't the economy just soak up all that "cheap" excess energy?
This thread is in the pseudoscience section because you guys failed to make any convincing, logical argument against the Etp model or its stark implications. The management was getting embarrassed and felt they needed to step in. They want the Etp model suppressed and they will do anything to accomplish their nefarious goal.*
Good timing too, since the markets are about to crash!
*I feel it is acceptable to speculate freely on the conspiracy to suppress the truth of the coming apocalypse, since we are now in the pseudoscience section. I hope that is okay.
---Futilitist
(shakes head)-- MY GOD-- how pathetic are you actually ?
my simple question of all of this is, why does not wall street use this etp model if it is so accurate, or oil companies in general?-- no one on wall street has even come across this shiit.
well, if the joke is coming from a joke-- then one should assume that anything that they state is therefore a joke.
he is referring to QE(again--his data is out of date).
he is referring to two different time frames in one moment-- right now we have a glut, but years from now--we will not have oil to be glutted--is what he is saying.
(shakes head)---what a pathetic joke you truly are..
exchemist
Valued Senior Member
That is because what you are looking for is not there. It is not necessary to evaluate the energy content of the oil being produced. The energy content of a barrel of oil never changes. It is the same as it has always been. What changes is the amount of energy required to produce the next barrel. That rises because of rising entropy production in the petroleum processing system. The Etp model measures rising entropy by using the Entropy Rate Balance Equation for Control Volumes, which is a second law statement.
No.
---Futilitist
How, then, can the model say the energy produced is insufficient for the energy needed in production? You obviously have to show both numbers and that one is greater than the other. Where are they and where is the expression showing the relationship between them?
Last edited:
Wow. Not that this thread has ever been particularly rational, but the diarrhea of the mouth in the past few days has gone to a new level. The arguments used to be just wrong and stupid, but now it seems you are intentionally making them gibberish, Futi. At one time when you would say "the economy is collapsing" you'd at least point to a GDP number. You were always wrong, but at least you made an effort to keep yourself connected to reality. But not anymore. Not only are you not referencing data anymore, but now you are making clear claims and then making up absurd definitions for the words after being asked for the references. Why? You can't possibly believe this stuff you are spewing anymore. What are you getting out of this? Have you blown a fuse?
Last edited:
Ok, lets look at it in rough numbers.
The average cost of producing 1 barrel of oil in the US is about $52 and the average cost of producing 1 barrel of oil in Saudi Arabia is $10.
This includes the costs involved with building oil facilities, pipelines and new wells. Also included in the cost are the costs of lifting oil out of the ground, paying employee salaries and general administrative duties.
Energy in 1 barrel of oil is approimately 1,700 kWh of energy.
The cost of energy in the US on average is $.12 /kWh.
At a cost of $52 dollars a barrel that equates to 433 kWh.
So the energy expended to produce 1 barrel of oil is only about 25% of the amount of specific energy in 1 barrel of oil.
For the Saudi Arabian oil it is about 5%.
So according to the the EPT model we are in fine shape and the 4 horsemen are going to have to put their horses out to pasture for a while longer.
Sorry the disapointing news that the world is not going to end soon Futilitist.
This has been fun but I need to go and enjoy my last few days before the apocalypse (just in case I made a math error).
Last edited:
exchemist
Valued Senior Member
Ok, lets look at it in rough numbers.
The average cost of producing 1 barrel of oil in the US is about $52 and the average cost of producing 1 barrel of oil in Saudi Arabia is $10.
This includes the costs involved with building oil facilities, pipelines and new wells. Also included in the cost are the costs of lifting oil out of the ground, paying employee salaries and general administrative duties.
Energy in 1 barrel of oil is approimately 1,700 kWh of energy.
The cost of energy in the US on average is $.12 /kWh.
At a cost of $52 dollars a barrel that equates to 433 kWh.
So the energy expended to produce 1 barrel of oil is only about 25% of the amount of specific energy in 1 barrel of oil.
For the Saudi Arabian oil it is about 5%.
So according to the the EPT model we are in fine shape and the 4 horsemen are going to have to put their horses out to pasture for a while longer.
Sorry the disapointing news that the world is not going to end soon Futilitist.
This has been fun but I need to go and enjoy my last few days before the apocalypse (just in case I made a math error).
Well yes you and I might think that but Fute says we are wrong.
So we need Fute to show us, from the ETP model, what the two numbers are according to that model. I don't see any values, and I don't even see any expression containing them.
There is a fairly significant error in your calc: you are comparing oil, which is a primary source of energy, with electricity, which is a secondary source. Electricity is made with about 33% efficiency, so your factors (which are the inverse of EROI) are high by a factor of 3: the expenditure of energy to produce oil in the USA is only 8% of the energy produced.
Googling for EROI stats will verify that, but be careful of out-of-date stats on fracking: it is a lot easier than people realized even 5 years ago.
But yeah, the point remains the same: we're so far away from the breakeven point that it isn't a common/relevant topic of discussion. That's why you don't regularly see it discussed in the media. Futie takes that silence and fills it in with falsehoods and gibberish.
Last edited:
Wow.
It is really great to see how popular this thread has suddenly become, but I must admit that I am getting a bit overwhelmed by the sheer volume of the response to this topic. I step away for just a second, and when I come back, I find a dozen high quality comments absolutely filled with intriguing and thought provoking questions to answer! There just is no way for me to address them all personally. So I have decided to hire an assistant. As soon as I have done this, I will be right back to give all of your super important questions the attention they deserve. Till then, feel free to discuss amongst yourselves.
---Futilitist
It is really great to see how popular this thread has suddenly become, but I must admit that I am getting a bit overwhelmed by the sheer volume of the response to this topic. I step away for just a second, and when I come back, I find a dozen high quality comments absolutely filled with intriguing and thought provoking questions to answer! There just is no way for me to address them all personally. So I have decided to hire an assistant. As soon as I have done this, I will be right back to give all of your super important questions the attention they deserve. Till then, feel free to discuss amongst yourselves.
---Futilitist
Last edited:
exchemist
Valued Senior Member
Wow.
It is great to see how popular this thread has suddenly become, but I must admit that I am getting a bit overwhelmed by the sheer volume of the response to this topic. I step away for just a second, and when I come back, I find a dozen high quality comments to answer! There just is no way for me to address them all personally. So I have decided to hire an assistant. As soon as I have done this, I will be right back to answer all of your important questions. Till then, feel free to discuss amongst yourselves.
---Futilitist
Thanks. We note the preparatory groundwork for an evasion, but naturally hope to be shown to be unduly cynical. I expect this means that you will now run off to B W Hill to try to get an answer - which is fine actually. If you don't understand the model yourself, talk to its creator. It makes sense. Let's hear what he has to say.
No, that's not how I read it at all. I read it as a mocking blow-off. I'm not sure if it means he's scuttling back under his rock for another 6 months or is just going to keep flooding and ignoring, but either way, he's blowing off what was basically just two simple and straightforward requests repeated by several different people (or you could even say it was one request for him to substantiate his two claims).
exchemist
Valued Senior Member
Well, I am trying to give the most generous interpretation I can, seeing that we are under the eye of the moderator now.
The days of "blowing off" are, I hope, over. Fute is on notice that he has to support his statements now, so let's see what he can come up with.- Status