No. The laws of physic have nothing to say about the price of anything, including oil; and Saudis do have a lot of control over the price of oil when that is twice or more than their production cost, as now. That is another serious defect in the etp model - fails to recognized production and demand systems change. For example the etp model of whale oil price, if once valid, is not valid anymore as we now have electric lights.
That is silly, Billy T. We stopped using whale oil when we started using crude oil. This transition resulted in a net energy gain for civilization. The situation is very different this time since we don't have a better energy source readily available to make a transition to.
As long as you are here, please take a look at this:
"Crude oil is used primarily as an energy source; its other uses have only minor commercial value. To be an energy source it must therefore be capable of delivering sufficient energy to support its own production process (extraction, processing and distribution); otherwise it would become an energy sink, as opposed to a source. The Total Production Energy ($$E_{TP}$$) must therefore be equal to, or less than EG, its specific exergy. To determine values for $$E_{TP}$$ the total crude oil production system is analyzed by defining it as three nested Control Volumes within the environment. The three Control Volumes (where a control volume differs from a closed system because it allows energy and mass to pass through it's boundaries) are the reservoir, the well head, and the Petroleum Production System (PPS). The PPS is where the energy that comes from the well head is converted into the work required to extract the oil. The PPS is an area which is distributed within, and throughout the environment. It is where the goods and services needed for the production process originate. This boundary make-up allows other energy, and mass transfers to be considered as exchanges, such as natural gas used in refining, electricity used in well pumping, or water used for reservoir injection."
~BW Hill
Values for $$E_{TP}$$ are derived from the solution of the
Second Law statement, the
Entropy Rate Balance Equation for Control Volumes:
$$\frac{dS_{CV}}{dt}
=\sum_j\frac{\dot{Q}_{j}}{T_{j}}
+\sum_i\dot{m}_{i}s_{i}
-\sum_e\dot{m}_{e}s_{e}
+\dot{\sigma}_{cv}$$
"Where $$\frac{dS_{CV}}{dt}$$ represents the time rate of change of entropy within the control volume. The terms $$\dot{m}_{i}s_{i}$$ and $$\dot{m}_{e}s_{e}$$ account, respectively, for rates of entropy transfer into and out of the control volume accompanying mass flow. The term $$\dot{Q}_{j}$$ represents the time rate of heat transfer at the location on the boundary where the instantaneous temperature is $$T_{j}$$. The ratio $$\frac{\dot{Q}_j}{T_j}$$ accounts for the accompanying rate of entropy transfer. The term $$\dot{\sigma}_{cv}$$ denotes the time rate of entropy production due to irreversibilities within the control volume."
~(Taken from
Fundamentals of Engineering Thermodynamics by Moran and Shapiro)
Because there is only one temperature boundary (at the exit point of the reservoir) and no crude oil enters the reservoir from the environment, the equation reduces to:
$$\frac{dS_{CV}}{dt}=\frac{\dot{Q}_{j}}{T_{j}}-\dot{m}_{e}s_{e}+\dot{\sigma}_{cv}$$
giving: $$\frac{BTU}{sec*°R}$$
For this application, crude oil and water can be treated as incompressible substances. Their specific entropies are only affected by a temperature change.
For specific heats: $$c_{v}=c_{p}=c$$, and $$s_{2}-s_{1}=c*\ln{\frac{T_{2}}{T_{1}}}$$ The reservoir temperature is constant, therefore the entropy of the reservoir must decrease at the same rate that the entropy is transferred from the reservoir by mass flow. Thus, the heat leaving the reservoir is negative in sign and the equation becomes:
$$\frac{\dot{Q}_{j}}{T_{j}}=\dot{\sigma}_{cv}$$
giving: $$\frac{BTU}{sec*°R}$$
The rate of entropy production in the petroleum production system is equal to the rate of heat extracted from the reservoir divided by the reservoir temperature.
The rate of irreversibility production in the petroleum production system therefore becomes:
$$\dot{I_{cv}}=T_{O}*\dot\sigma_{cv}$$
giving: $$\frac{BTU}{sec}$$
Where $$T_{O}$$ equals the standard reference temperature of the environment, 537 °R (77° F).
Therefore:
$$E_{TP}=\int_{t1}^{t2}\dot{I_{cv}}dt$$
giving: $$BTU$$
Because the mass removed from the reservoir is limited to crude oil and water, the increase in $$E_{TP}$$ per billion barrels (Gb) of crude extracted as $$ds=c\frac{dT}{T}$$ is:
(
Equation#7)
$$\frac{E_{TP/lb}}{Gb}
=\begin{bmatrix}\frac{(m_{c}*c_{c}
+m_{w}*c_{w})(T_{R}-T_{O})}{m_{c}} \end{bmatrix}/Gb$$
giving:
BTU/lb/Gb
$$m_{c}$$ = mass of crude, lbs.
$$c_{c}$$ = specific heat of crude, BTU/lb °R
$$m_{w}$$ = mass of water, lbs.
$$c_{w}$$ = specific heat of water, BTU/lb °R
$$T_{R}$$ = reserve temperature, °R
$$T_{O}$$ = standard reference temperature of the environment, 537 °R
$$s_{i}$$ = specific entropy into the control volume
$$s_{e}$$ = specific entropy exiting the control volume
BTU/gal/Gb for 35.7° API crude = BTU/lb/Gb * 7.0479 lb/gal
Evaluation of $$E_{TP}$$ from
Equation# 7 requires the determination of three variables: mass of the crude ($$m_{c}$$) mass of the water ($$m_{w}$$), and the temperature of the reservoir ($$T_{R}$$). These must be determined at time (t).
1) The mass of crude at time (t) is derived from the cumulative production function,
2) the mass of water is derived from the average % surface water cut (fw) of the reservoir,
3) temperature of the reserve is derived from the well depth. This assumes an earth temperature gradient of 1°F increase per 70 feet of depth.
-------------------------------
What do you think of the methodology used to create the Etp model?
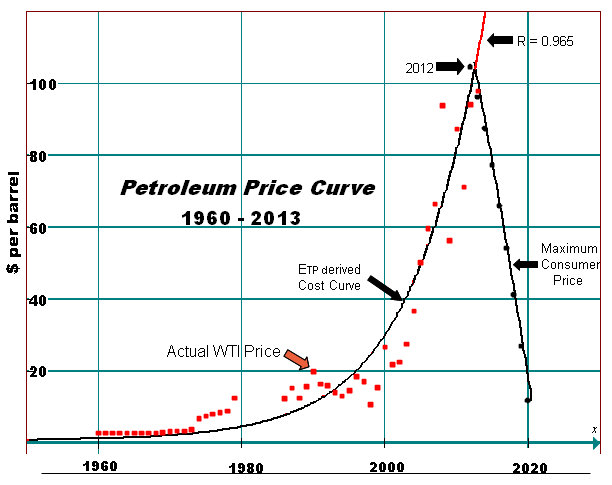
How do you explain the fact that the Etp model forecast the price of oil from 1960-2009 with an accuracy of 96.5%?
---Futilitist