Logical argument using infinity

[Sarkus]

The issue I see with the argument is that it basically treats infinity as a number.
It is true that as the radius of the circle gets larger and larger the circumference appears straighter and straighter, but infinity is not a number where one can go "so at infinite radius it is a straight line" but rather it is a limit... a limit that is never actually met.
This is why calculus works, by taking smaller and smaller elements that approach zero, but never actually are zero.
So if the OP doesn't treat infinity as a number, the issue goes away because the conceptualisation becomes more aligned with reality.

The other issue with infinities is that they are not all the same.
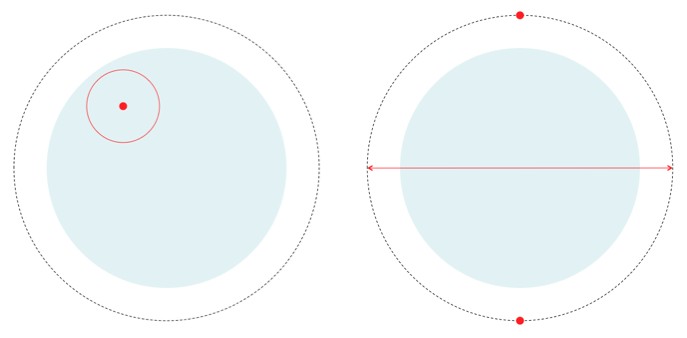
A circle with infinite radius will still have a circumference equal to 2*pi*radius. At infinit radius th circumference is also infinite, but it is not the same length as the radius.
Similarly the set of positive integers is infinite, and twice as large as the set of even numbers, even though the latter is also infinite in size.
Infinity is a concept, a useful one in mathematics, but it is not a number.

 

[Neddy Bate]

^ Yes, that makes sense.

Also, my post #20 should have said "fewer and fewer degrees" not "fewer and degrees," my bad.

 

[arfa brane]

A circle with infinite radius will still have a circumference equal to 2*pi*radius.

I don't think so.
It won't have a circumference equal to a constant times infinity, because that makes no mathematical sense. Like I said, there is no ratio between the circumference and the diameter when you "get to" an infinite radius.

The other detail you may have noticed, is that if pairs of perpendicular lines are 180° apart where they are tangent to a circle with infinite radius, then they must be perpendicular to themselves also, because each line is parallel to itself.

This can be "explained away" if you accept that the infinite circle wraps around itself, as that quote I posted says.

 

[arfa brane]

infinity is not a number where one can go

It may well be true that infinity is not a number, however, it is a place you can project lines to. So the lack of "numericity" doesn't prevent one from claiming an infinite line exists, and that it's equivalent to a circle with infinite radius.

Notice how this circle can be said to have a centre where two lines intersect (which need not be perpendicular), or a centre at infinity. In fact, the centre of an infinite circle is at the centre of the plane (i.e. nowhere in particular, or everywhere).

 

[Write4U]

Can there be an infinitely small arc?

I don't think so.
It won't have a circumference equal to a constant times infinity, because that makes no mathematical sense. Like I said, there is no ratio between the circumference and the diameter when you "get to" an infinite radius.

I agree describing a circle that way makes no mathematical sense. That's why it is not possible in reality.
A circle is an ideal pattern just like all Platonic solids. Increase any Platonic solid to infinite size and they all lose their form and mathematical identification. They are ideal forms.

The other detail you may have noticed, is that if pairs of perpendicular lines are 180° apart where they are tangent to a circle with infinite radius, then they must be perpendicular to themselves also, because each line is parallel to itself.

This can be "explained away" if you accept that the infinite circle wraps around itself, as that quote I posted says.

So, in order to make it work, we must assume that at some stage a circle must have a circular pattern which answers to Pi, no? If not, can it still be called a circle, or a triangle, or a cube? Or just Infinite in size ?

 

[Sarkus]

I don't think so.
It won't have a circumference equal to a constant times infinity, because that makes no mathematical sense. Like I said, there is no ratio between the circumference and the diameter when you "get to" an infinite radius.

Yes, there is still a relationship, and it is that the circumference is 2*pi*radius. This doesn't change as you approach the infinite radius. Yes, the circumference also approaches infinite as the radius approaches infinite, but the relationship still holds. It has to hold or you are no longer describing a circle, and if you aren't describing a circle then to speak of "a circle with infinite radius" is meaningless.
The reason you don't agree is because you are treating infinity like a number, and not just that but a number where all infinities are equal. They aren't. As already explained.

 

[Write4U]

Yes, there is still a relationship, and it is that the circumference is 2*pi*radius. This doesn't change as you approach the infinite radius. Yes, the circumference also approaches infinite as the radius approaches infinite, but the relationship still holds. It has to hold or you are no longer describing a circle, and if you aren't describing a circle then to speak of "a circle with infinite radius" is meaningless.

Question: then what does it mean to have arcs become straight and the circle attains parallel sides, which are no longer equi-distant from the center?

The reason you don't agree is because you are treating infinity like a number, and not just that but a number where all infinities are equal. They aren't. As already explained.

Especially if you cannot even establish a physical center......

 

[NotEinstein]

There's more trouble on the horizon though...

A circle is defined as the set of points that are equidistant from a fixed/specific point (called its center). And let's use the rules set out by arfa brane.
Suppose we have a circle of radius infinity. Pick a point on the circle. Take a one-unit-distance step towards the center. The distance of this new point is infinity minus one = infinity. That distance-to-the-center is equal to the set radius of the circle, so this new point is also part of the circle. Repeat this, in any direction you want, and you'll find that any point an arbitrary number of steps away from our original starting point is part of circle.
This part of the circle's arc is thus a plane, not a straight line!

Conclusion: infinite radius circles are ill-defined.

 

[arfa brane]

Suppose we have a circle of radius infinity. Pick a point on the circle. Take a one-unit-distance step towards the center. The distance of this new point is infinity minus one = infinity. That distance-to-the-center is equal to the set radius of the circle, so this new point is also part of the circle. Repeat this, in any direction you want, and you'll find that any point an arbitrary number of steps away from our original starting point is part of circle.
This part of the circle's arc is thus a plane, not a straight line!

There are problems with all that too.

As mentioned, the centre of a circle with infinite radius is the centre of the plane; where is that? You appear to be assuming you can move a unit distance towards this centre.

Unfortunately a unit distance is not meaningful at infinity . . .
Also unfortunate is that the direction towards the centre is not meaningful (where is the centre?) . . .

Therefore the relation between the circle's circumference (infinite) and its diameter (also infinite) is not meaningful despite Sarkus' objections.

However, the notion of a circle at infinity is not ill-defined, at least not in projective geometry. And calculus lets you get away with circles with an infinite radius. Another detail is that choosing a point on the infinite line (circle) means you choose two points, which are antipodal.

 

[James R]

A circle with infinite radius will still have a circumference equal to 2*pi*radius. At infinit radius th circumference is also infinite, but it is not the same length as the radius.

This is the problem with transfinite arithmetic that I alluded to earlier.

Technically, the cardinality of the two infinities - the circumference and the radius - of the infinite circle, is the same, so in a specific sense the circumference is the "same" as the radius for an infinite circle. However, it is still $2\pi$ times as large, at the same time! The "problem", roughly speaking, is that "two times infinity equals infinity".

Similarly the set of positive integers is infinite, and twice as large as the set of even numbers, even though the latter is also infinite in size.

Again, it turns out that the cardinality of the set of all even numbers is the same as the cardinality of the set of all integers, because the elements of the two sets can be put into a one-to-one correspondence (i.e. every element in the set of integers can be paired with a single, unique element in the set of even numbers). So, in a sense, there are "just as many" even numbers as there are integers.

Infinity is a concept, a useful one in mathematics, but it is not a number.

There's an entire sub-field of mathematics devoted to transfinite numbers, so it's not "just" a concept. It can be made more precise.

For example, the classic result is that the infinity of the real numbers is provably larger than the infinity of the integers - a result due to Cantor. i.e. not all infinities are the same, but some are.

It won't have a circumference equal to a constant times infinity, because that makes no mathematical sense. Like I said, there is no ratio between the circumference and the diameter when you "get to" an infinite radius.

Sensibly, the ratio of the circumference to the diameter is $\pi$, no matter how large your circle is. But that doesn't necessarily mean the circumference is "larger" than the diameter, since we're dealing with two transfinite numbers.

The other detail you may have noticed, is that if pairs of perpendicular lines are 180° apart where they are tangent to a circle with infinite radius, then they must be perpendicular to themselves also, because each line is parallel to itself.

This is the point where I disagree with you. I don't think that your pairs of perpendicular lines suddenly become parallel when you blow the radius of your circle up to infinity.

This can be "explained away" if you accept that the infinite circle wraps around itself, as that quote I posted says.

All circles wrap around themselves and come back to where they started. Head off around the circumference of a circle and you must eventually find yourself back at your starting point. Making the circle infinite doesn't alter that fact. It just means it might take you a bit longer to go round (like, as in, infinitely longer!).

 

[arfa brane]

This is the point where I disagree with you. I don't think that your pairs of perpendicular lines suddenly become parallel when you blow the radius of your circle up to infinity.

Well they do, if it's true that the perpendicular lines are tangent to a circle and remain tangent to it even when the radius of the circle is infinite.
Otherwise we need to invent some rule that either makes perpendicular lines not tangent to the infinite circle--but that seems to introduce a bigger problem--or does away with tangents somehow.

Sensibly, the ratio of the circumference to the diameter is π, no matter how large your circle is.

Sensible doesn't seem to cut it with infinite circles, though.

All circles wrap around themselves and come back to where they started. Head off around the circumference of a circle and you must eventually find yourself back at your starting point. Making the circle infinite doesn't alter that fact. It just means it might take you a bit longer to go round (like, as in, infinitely longer!).

True. However not all circles have antipodal points identified; the infinite circle does because it's infinite.
Yes, really! Have you read anything at that link to stackexchange where several people discuss it?

How about this:

Parallel lines meet at two points on the horizon (in opposite directions). So the line at infinity is weirdly defined with opposite points on the horizon being the same point. Mathematicians would say “antipodal points are identified”. In the projective plane two lines always meet at one point.

No matter how big the circle is, or where its center is, the whole thing will always be in the plane (not all the way out to the line at infinity). If the circle does have a point on the horizon, then you’ll find that the center also has to be at infinity (if it’s in the plane, then it’ll be closer to some points on the circle than others, but the center point is the same distance to every point on the circle). Specifically, the center will be on the line at infinity exactly 90° away from where the circle intersects the line.

The projective plane, which includes the usual infinite plane (light blue) and the line at infinity (dashed line), and two examples of circles.
Note that, although the plane is infinite, the line at infinity wraps around it in the same way that the horizon would still wrap around you
even if the Earth were flat and infinite (this is an abstract picture).
Left: a circle and its center in the in the ordinary plane. Right: a circle that passes through the east-west point on the line-at-infinity.
Its center is at the north-south point on the line-at-infinity.
--https://www.askamathematician.com/2...e-with-an-infinite-radius-curved-or-straight/

 

[arfa brane]

One clue here is that the infinite circle, or circle with infinite radius is, as some have guessed, not really a circle. What it is is an infinite line.

But as the above diagram suggests, the infinite line is "really" a circle whose centre is undefined--"at infinity" in the Euclidean plane. There is no finite radius, no diameter, so π isn't just not defined, but can't be defined.

I say again, there are no constants, no units of distance, at infinity, and that's a logical conclusion.

 

[NotEinstein]

There are problems with all that too.

As mentioned, the centre of a circle with infinite radius is the centre of the plane;

(It's not established that the center of the circle is the center of the plane I described; what plane are you talking about?)

where is that? You appear to be assuming you can move a unit distance towards this centre.

Let's analyse what you just said. If the direction towards the center cannot be established, then it conflicts with the definition of a circle: the center of the circle needs to be a single, fixed point, and I can always draw a straight line between it and any other point. The center cannot be a collection of points in all directions, and no single point can lie in multiple directions. The only "out" I see is if the space in non-Euclidean or non-flat, but then we aren't doing simple geometry anymore.

Unfortunately a unit distance is not meaningful at infinity . . .

Exactly; so that straight line's width also "isn't meaningful", which was what I demonstrated. Your "straight line" can have an arbitrarily large finite width, which means it's a plane, not a straight line.

Also unfortunate is that the direction towards the centre is not meaningful (where is the centre?) . . .

Right, and therefore you are no longer in Euclidean space. Which is fine, except you were indicating you were using it in your OP.

Therefore the relation between the circle's circumference (infinite) and its diameter (also infinite) is not meaningful despite Sarkus' objections.

(No comment.)

However, the notion of a circle at infinity is not ill-defined,

I just demonstrated it is. You merely saying "na-ah!" isn't good enough; please provide arguments.

at least not in projective geometry.

As far as I'm aware, I didn't employ projective geometry, and neither did you in your OP, so I'm not sure what the relevance is?

And calculus lets you get away with circles with an infinite radius.

Please provide an example of this. Note that a circle with the radius being "a limit to infinity" isn't the same as a circle with infinite radius.

Another detail is that choosing a point on the infinite line (circle) means you choose two points, which are antipodal.

Yes, every single point you can pick on a circle will also have an antipodal point. Please explain why this detail is in any way, shape, or form relevant here?

 

[NotEinstein]

Wait, I just realized one more point I need to make...

Also unfortunate is that the direction towards the centre is not meaningful (where is the centre?) . . .

This is actually a red herring; as you can see from the conclusion of my argument, the direction towards the center is actually not relevant to the argument at all: all directions I take a step in result in the "infinite distance, thus part of the circle" bit. So if you don't accept that the center is in a particular direction, fine, leave that bit out of the argument, and it still works just fine.

 

[arfa brane]

all directions I take a step in result in the "infinite distance, thus part of the circle" bit.

Yes, quite. In fact the step you take could be an infinite step, yes? In that case you will step along the infinite-line/circle-with-centre-at-infinity.

Now all you need is a well-defined function that corresponds to such a step, so that any step can be either finite or infinite, all you need is a function that leaves you somewhere on the infinite line! That is, nowhere in particular, or anywhere.

 

[arfa brane]

the center of the circle needs to be a single, fixed point, and I can always draw a straight line between it and any other point.

When you say a single fixed point, what fixes this point? If it's the centre of a circle with infinite radius, how do you do this? Isn't it much easier to just assert the centre is the centre of the infinite plane? In that case the centre has no defined position; moreover it can't have one.

Exactly; so that straight line's width also "isn't meaningful", which was what I demonstrated. Your "straight line" can have an arbitrarily large finite width, which means it's a plane, not a straight line.

I can't follow this, sorry. A line has zero width, anywhere you can construct one.

Right, and therefore you are no longer in Euclidean space. Which is fine, except you were indicating you were using it in your OP.

Are you saying infinite circles don't exist in the Euclidean plane? Perhaps you mean you can't construct an infinite line in the plane? That would have to follow if the first thing is true, surely?

 

[Write4U]

Question; Can an arc be infinitely small without being absolutely straight?

 

[NotEinstein]

Yes, quite. In fact the step you take could be an infinite step, yes?

Yes, you potentially could. However, because it's not necessary for my argument, and due to all the complications it introduces, I purposefully excluded it. For example: if I take an infinite-sized step towards the center, can I reach it? In other words, what's infinity minus infinity?

In that case you will step along the infinite-line/circle-with-centre-at-infinity.

​

I'm not convinced you would necessarily step along the line. Let's say the line lies at an angle of 30 degrees; if I take an infinite (straight) step at 45 degrees from a point on the line, how can I end up back on the line? Euclidean geometry says that's not possible: two non-parallel straight lines can only have on intersection, and that's where I started from. Please explain how you see this being possible.

Now all you need is a well-defined function that corresponds to such a step, so that any step can be either finite or infinite, all you need is a function that leaves you somewhere on the infinite line! That is, nowhere in particular, or anywhere.

(No comment for now, as I don't see how this is relevant to our current discussion.)

When you say a single fixed point, what fixes this point?

It's in the definition of "circle". For example, Google defines a circle as: "a round plane figure whose boundary (the circumference) consists of points equidistant from a fixed point (the centre)."

If it's the centre of a circle with infinite radius, how do you do this?

Well, that's your problem, isn't it? You are saying this is possible to do, not me.

Isn't it much easier to just assert the centre is the centre of the infinite plane?

Again, what plane exactly? And how can an infinite plane have a well-defined center?

In that case the centre has no defined position; moreover it can't have one.

Again, you are the one claiming this is possible, not me.

I can't follow this, sorry. A line has zero width, anywhere you can construct one.

If finite distances have no meaning, how can the width of your line have meaning?
But let me illustrate. Let's go back to the center of the circle, and use this as the origin (0, 0) of a polar coordinate system (r, phi). The line is now at infinite distance (r = inf, where r is the coordinate, not the circle-radius). I take a point on this line (inf, phi). I then take a point that's one-unit-distance further away (so it's along the radial, coordinate: (inf + 1, phi)). This point is at a distance infinity plus one equals infinity. So it's also part of the "line", since it's in the same direction and has the same distance as a known point on the line (inf, phi); it has the same coordinates. I can repeat this an arbitrary number of times, and/or with steps of an arbitrary finite size, and thus determine the width of the "line" to be any finite width. And as such, it's not a line, because lines, as you said, have zero width.

Are you saying infinite circles don't exist in the Euclidean plane?

That's exactly what I'm trying to deduce with my argument, yes. I'm not claiming it though; it would be a conclusion drawn from the arguments made.

Perhaps you mean you can't construct an infinite line in the plane?

What? I have no idea how you read that into anything that I wrote here?

That would have to follow if the first thing is true, surely?

Please explain how you made that conclusion from what I wrote.

I see that you've chosen to ignore my request for example of circles with infinite radius in calculus, but at the same time you've chosen to ask me whether I think infinite circles can exist in the Euclidean plane. If you have any example, please provide them instead of trying to set an ambush for me.

 

[Speakpigeon]

Circle: a plane curve everywhere equidistant from a given fixed point called the center.

As I see it, infinity isn't a number. It's more like a condition, i.e. the condition that, in some aspect or dimension, there's no limit.
This in itself doesn't disqualify circles with an infinite radius but there are in effect infinitely many infinite circles, all different and all having, obviously, an infinite radius. Given each one is a circle, the points on a circle are equidistant from the centre, i.e. there is such a thing as the distance from each of these points to the centre, this distance just has to be infinite (and an actual infinite, i.e. a infinite distance between two points). As there is an infinity of infinite circles, there is therefore an infinity of infinite radiuses, all infinite but all different in lengths. All such infinite circles are essentially "ordinary circles" except for their infinite radiuses.
I think there isn't much point discussing these things because, again, there is an infinity of these things. So, which one are you talking about?
It's possible of course to do this properly. For example, we can easily conceive of an ordinary tube with two ends but infinitely long in between the two ends. At one end, it's just the section of the tube, which makes a perfect circle. At the other end, the tube gets a pointy end, literally. Now, think of this tube as a universe unto itself. There, you have a circle whose centre is the pointy head. That's just one simple example but we can see that in this case the circle is still essentially a circle, only its centre is an infinite distance away from it.
I don't think all such circles have any property in common beside that of ordinary circles and that of having an infinite radius.
EB

 

[Speakpigeon]

It seems to me that all Arf is doing when he lets the radius approach infinity

How does anything not infinite approach infinity, though...
EB