Logical argument using infinity

[arfa brane]

In geometry, a real projective line is an extension of the usual concept of line that has been historically introduced to solve a problem set by visual perspective: two parallel lines do not intersect but seem to intersect "at infinity".

For solving this problem, points at infinity have been introduced, in such a way that in a real projective plane, two distinct projective lines meet in exactly one point. The set of these points at infinity, the "horizon" of the visual perspective in the plane, is a real projective line.

It is the circle of directions emanating from an observer situated at any point, with opposite points identified. A model of the real projective line is the projectively extended real line. Drawing a line to represent the horizon in visual perspective, an additional point at infinity is added to represent the collection of lines parallel to the horizon.

--https://en.wikipedia.org/wiki/Real_projective_line

Ok, you say, this is from Wikipedia. Yes, but this is one of > 100,000 hits I get when I google "circle of directions".

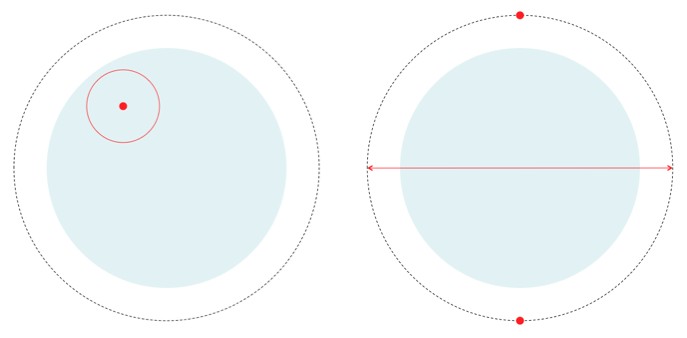
So yeah, ok then. The infinite line (the dashed line in the diagram), is a set of parallel lines. I knew that. In fact it makes sense--a line at infinity must have lines parallel to it, also at infinity. This follows because a circle with finite radius with a single point on the infinite boundary, has its centre on the boundary (because the finite radius doesn't exist at infinity).

So now, how does the diagram of the projective plane (which is still the Euclidean plane), map to a sphere? How is the sphere topologically the plane?

 

[Write4U]

The infinite line (the dashed line in the diagram), is a set of parallel lines.

Huh?
a) parallel lines are at equal-distant from each other at every point.
b) a circle does not have intersecting lines, it has a single continuous line.

I see no reason why this should not be true in the abstract as it is mathematically defined in physics.

 

[arfa brane]

Huh?
a) parallel lines are at equal-distant from each other at every point.
b) a circle does not have intersecting lines, it has a single continuous line.

I see no reason why this should not be true in the abstract as it is mathematically defined in physics.

But a) the infinite line must have lines parallel to it because it's a straight line; if it's also at infinity then "equal distance" doesn't really make sense, although parallel still does.
b) A circle can intersect the infinite (projective) line.

The projective plane and the complex projective plane are quite common in physics. How do you project the gravitational potential of some mass to infinity? Or why would you want to?

 

[arfa brane]

Another logical argument:

Suppose you have an infinite line in the plane; that means both ends of the line are extended to infinity.

For a circle tangent to this extended line at one point, the centre will be a finite distance from this infinite line. As the radius of any circle gets larger, the circle tangent to the infinite line will get straighter (i.e. less curved). As the radius of any circle increases without limit, the circle itself will approach a straight line.

When the centre of the circle is an "infinite distance" from the line it is tangent to, the circle will be parallel (and collinear) with the infinite line.
Then the infinite line is the boundary of an "infinite circle" whose centre can only be defined as being at the centre of the infinite plane. (See the diagram with the dashed circle on previous pages)

There the tangent point for such a circle is two antipodal points on the infinite circle of directions (defined at every point in the plane).

 

[arfa brane]

This is my original construction, circles tangent to a pair of perpendicular lines.

So my argument goes, each circle's centre lies on the diagonal line, y = x, and this line passes through each circle twice.
Start with a family of distinct circles, whose centres are defined by a geometric function (in my diagram, this gives x = 2,4,8, ... ) with a closed form and then sum from 1 to n, so that there are 2n intersections along y = x.

If the sum goes to infinity though, things change, there are infinite intersections and infinite centres, most of them at infinity (??). This is where the infinite set of parallel infinite lines is.

 

[James R]

If the sum goes to infinity though, things change, there are infinite intersections and infinite centres, most of them at infinity (??)

What do you mean by "things change"? What things change?
Also, arguably none of the individual intersections is "at infinity". For any value of n, there are two intersections between the line y=x and the circle in question, and the coordinates of the intersection points do not involve infinity. Infinity is only a kind of limit of the sequence you've set up.

 

[arfa brane]

For any value of n, there are two intersections between the line y=x and the circle in question, and the coordinates of the intersection points do not involve infinity.

Not quite; your statement holds for finite n. It could be reworded as "when n has a value . . ."; if n isn't finite, it doesn't have a value (at least, not a finite one).

The logic isn't hard to follow here: what happens if you project a line in the plane at both ends? What does "going to infinity" mean? Can you "come back" if you get there, and when are you at infinity? Why do I need to define a function here and give it a limit at infinity?

If you have an infinite line as I've laid out, then you can easily construct circles tangent to this line. If as the circles get larger (and I've defined a sequence such that successive centres are farther apart on the line y = x) they get straighter, when straight they must be infinite. This idea that an infinite line is also an infinite circle is something I first encountered in calculus in the year 1980. What's the problem here?

Why would anyone claim there is only one type of curve with constant curvature? That is, circles with a finite radius, and lines (or "infinite" circles).
Why can you have a circle of directions at a given point and why don't you need to construct an actual circle to prove it exists?

When you take an infinite limit, like $$\lim_{n \to \infty} $$ for some function of n, is infinity numerically defined? If it isn't, how is the limit even defined? What about $$ \sum_{n=1}^{\infty} $$, or infinite sums (polynomials)?

 

[arfa brane]

what happens if you project a line in the plane at both ends?

. . . it extends to infinity in two opposite directions.

What does "going to infinity" mean? Can you "come back" if you get there, and when are you at infinity?

See above. If you are somewhere on an infinite line, you are not at infinity (as if that helps). . .

Why do I need to define a function here and give it a limit at infinity?

Don't ask me, all I need is the idea of a line which "is" extended.

 

[arfa brane]

My OP started out with the claim the Euclidean plane is infinite in extent. Is there a way to prove this without introducing points or lines with a constant length?

If the plane is somewhere you can construct circles and so "prove" that points and lines with constant distance both exist, where is the plane?
The plane is wherever you need it to be. But if the real number line is infinite, it follows that the plane is too.

Since a line can be infinite in the plane, it follows also that the choice of a unit distance is completely arbitrary, and completely localised (to where unit circles make sense, say); most of the remainder of the infinite line is "at infinity" (where your units aren't).

So if it makes sense to talk about two different parts of an infinite line, but infinitely separated, it follows that Euclidean distance is affine.

 

[arfa brane]

Another look at the diagram.

Say you consider a slice of the diagram instead of the whole thing, the slice corresponding to the horizontal strip the red line is inside of (in the right hand image). The two ends of this strip are finite parts of the infinite line and so, from an infinite 'perspective' have zero length.

The red line is drawn as if it separates the affine plane into two equal parts, and as if it passes through a central point. This is a problem because infinity divided in half is still infinity.

 

[arfa brane]

I also realised the diagrams have another representational problem. The blue discs are finite representations of the infinite plane (or the centre of the plane).

You could define this as the set of points from which all lines project to infinity (or the dashed line), in two directions. So each point has this abstract 'circle of directions' defined on it. Technically the infiniteness of the plane means that finite distances vanish at infinity (or at a total 'infinite' perspective, which the blue discs are meant to be).

So the left hand diagram has a finite circle in it, which technically can't be represented if the space is meant to be being seen "from infinity". The "circle" in the right hand diagram is a different story, the red line is infinite.