I'm not making anything up. As for that century of mathematics and experiment, it's the Schrodinger wave equation. The Dirac equation is a relativistic wave equation. E=mc² is not in doubt, and nor is a radiating body loses mass. Pair production is a totally legit experiment, so is electron diffraction, and atomic orbitals where electrons exist as standing waves, and the Einstein-de Haas effect, and and electron-positron annihilation to gamma photons. The wave nature of matter is not in doubt. The wave nature of the electron is not in doubt. And that wave isn't going thataway → at c, now is it? What's "almost medical" is that despite all the above, somebody will now jump into the conversation and tell you the electron is a point-particle. Groan.
do the particles ever collide in QED
- Thread starter Arlich Vomalites
- Start date
But you clearly are: you have admitted that there isn't anyone who is presenting the light-vortex-curved-space idea that you are promoting. It's your idea alone.
You cannot both claim to endorse the scientific results and at the same time ignore the details of those results that make your idea look dubious. If you were serious about science, you would learn how to do it and compare your ideas to experiment.
exchemist
Valued Senior Member
Relax, nobody is questioning the wave-like nature of matter. But this stuff of yours about an unbound electron being represented as a standing wave is made up.
Schroedinger's equation in its general (time-dependent) form is not a wave equation: it is a diffusion equation. (This is because it has only a first, rather than second derivative with respect to time). It is only the time-independent form, which is the version applicable to stable, bound states that has the form of a standing wave equation - because under those conditions you have something analogous to a standing wave.
That is why I am pointing out that you are making things up. You need to learn this stuff properly and to stop just talking out of your arse.
Lord knows, I am not the right person to answer this question. But let me throw a few balls in the air and see if they land in any sort of pattern......
The Lie group SU(2), like any Lie group, describes continuous symmetries. In this case these symmetries take the {possibly) unusual form of rotations such that $$x = 4\pi x$$
Now every Lie group is entitled to an algebra, which for technical reasons is a vector space whose basis vectors we may write as $$X,\,Y,\,Z$$. Again for technical reasons we require these, in their 2 x 2 matrix representations, to be anti-Hermitian.
So consider the Hermitian Pauli matrix $$\sigma_z$$. Then we can make the Hermitian matrix representation of $$\sigma_z$$ to be anti-Hermitian simply by multiplying the unit $$i$$. So $$i \sigma_z = Z$$ more or less as a convenience.
Now one recovers any Lie group from its algebra (vector space bases) via the exponential map $$\exp (X) \in SU(2)$$.
So it may - just may - be that the Pauli matrices have the "physical significance" that they likewise describe continuous rotational symmetries of the form $$x=4 \pi x$$.
Sure looks like spin one half to me. But I just "made that up" and it may be wrong
exchemist
Valued Senior Member
Phew! I'll need to go away and re-read my Quantum Chemistry books now and see if any of that relates to what you are saying. The terminology is vaguely familiar but it was all a long time ago.
I do recall that whilst physical observables are always represented by Hermitian operators, the converse is not always true - hence my question. I also recall that in the treatment of angular momentum there are funny things called shift (raising and lowering) operators, which have no physical significance but are used to generate the family of possible states. That's the general area I'll try re-reading, anyway……...
It isn't made up. Knock an electron out of an atomic orbital. It doesn't disappear at c, now does it? It doesn't decay does it? And you can diffract it, can't you?
Was there some part of it doesn't disappear at c, it doesn't decay, and you can diffract it that you somehow missed? And let's take a look at Wolfram shall we? "The Schrödinger equation is the fundamental equation of physics for describing quantum mechanical behaviour. It is also often called the Schrödinger wave equation, and is a partial differential equation that describes how the wavefunction of a physical system evolves over time." How about hyperphysics? "It is a wave equation in terms of the wavefunction which predicts analytically and precisely the probability of events or outcome." Or how about this star garden: "In 1926, Austrian physicist Erwin Schrödinger reasoned that if electrons behave as waves then it should be possible to describe them using a wave equation, like the equation that describes vibrations of strings or Maxwell's equation for electromagnetic waves." How about the physics stack exchange: "The Schrodinger equation is a wave equation, not a diffusion equation. While the equations look similar, the i in Schrodinger equation differentiates them; that allows non-decaying oscillatory solutions, which diffusion equations do not allow."
I'm not. But you are dismissing all the evidence and the references, and huffing and puffing and bullshitting to cover up your chemist's ignorance of physics. Now listen up: the electron has a wave nature, whether it's inside an orbital or not. Which is why Ehrenberg and Siday were able to write The Refractive Index in Electron Optics and the Principles of Dynamics. Not only can you diffract electrons, you can refract 'em. As you will doubtless be unaware, this paper predicted what is now know as the Aharonov-Bohm effect which "is accordingly illustrated by interference experiments".
Try $$ x = \frac{1}{\sqrt{c^3}}$$ and get your calculator out. Don't worry about the dimensionality.
Good answer! I'm not as comfortable with Lie algebras as I should be, but I think this squares with what I know. A couple of additions:
On first reading, I thought you were saying that any Lie algebra needs to have basis vectors in $$X,\,Y,\,Z$$, and that the 2x2 matrix representation specifically always needs to be anti-Hermitian. I don't think that's what you meant to say, but I'd like to clarify that it's not correct. The particular Lie algebra describing the rotational symmetries of a sphere has these properties, but in general one can have Lie groups in larger spaces with bigger matrices. For instance, the Gell-Mann matrices are a group of eight 3x3 matrices that look like "generalized Pauli matrices" and describe the rotation symmetries of SU(3); they are useful in, among other things, describing the spin of a photon.
Second, I think it's illustrative to note that the Pauli matrices are just one of infinitely many choices of bases that could describe SU(2). We use them because they're convenient to write, but just as 3D space can be spanned by any set of 3 orthogonal vectors, so SU(2) can be described by any set of 3 orthogonal, 2x2, anti-Hermitian matrices. (Two matrices are orthogonal if the trace of their product is zero.) By summing the Pauli matrices according to:
$$\sigma_{\theta,\phi}=\cos(\theta)\sigma_z+\sin(\theta)\cos(\phi)\sigma_x+\sin(\theta)\sin(\phi)\sigma_y$$
we can produce a Pauli matrix for rotation about the arbitrary axis given by the angles $$\theta$$ and $$\phi$$. By extension, we can multiply by $$\hbar/2$$ to get the matrix for measuring electron spin in that arbitrary direction. With three such rotated Pauli matrices, we can describe SU(2) in terms of rotations about tilted coordinates, using matrices that are messier but no less valid than the traditional Pauli matrices. I think this gives some intuitive insight into why the Pauli matrices are so closely related to spin: each Pauli matrix describes rotation about some axis in a unitless way, and to get electron spin out from a unitless rotation, we simply need to multiply by the united quantity $$\hbar/2$$ to specify how "big" the spinning is.
exchemist
Valued Senior Member
Farsight, I am perfectly content to let readers to judge who, in this interaction, is "huffing and puffing and bullshitting".
I am also content to let readers judge the degree to which I know what I am talking about, and my behaviour when I think I have reached the limits of my knowledge.
It doesn't matter what readers think. What matters is the physics and the evidence and the mathematics that I've referred to. That you're just ducking because it doesn't square with some kindergarten popscience you were spoonfed when you were a kid. Perhaps you need to pay attention to some of the things Fednis said:exchemist said:
I don't suppose that will help? No? Lordee save us from chemists pontificating about physics.
exchemist
Valued Senior Member
…not to mention self-taught IT blokes from Portsmouth with a candle-lit shrine to Einstein in the garage
.
Since you have admitted to not knowing the relevant mathematics, I agree that the mathematics you referred to matters.
Poole. Not Portsmouth. This is the place:
And there is no candle-lit shrine to Einstein. Or Maxwell. Or Newton. Or Feynman. Et cetera. Now, you've conceded the wave nature of matter. So what is this wave doing? Is it going thataway → at c? Since the electron is just sitting there in front of you, I guess that's a no. So what else can that wave be doing? I know, let's see if Fednis can offer us a clue:
And there is no candle-lit shrine to Einstein. Or Maxwell. Or Newton. Or Feynman. Et cetera. Now, you've conceded the wave nature of matter. So what is this wave doing? Is it going thataway → at c? Since the electron is just sitting there in front of you, I guess that's a no. So what else can that wave be doing? I know, let's see if Fednis can offer us a clue:
Hmmn. Nope. I know, the electron must be a point particle then!Fednis48 said:
None of these inferences about the nature of the electron have anything to do with your idea that an electron is a photon.
Show us how to diffract a spindle-sphere torus so that it remains a spindle-sphere torus. If you can't do this, then your idea can't work.
So, to be clear, you are claiming that a photon is a bound state of a photon. Just trying to get you to commit to details.
If "we" do, we see that you quote only the part where the names including the term "wave" are used. That something can be called a "wave equation" and also be something else seems to elude your understanding, because you are only doing textual analysis, not physics.
I am not surprised that you do not understand complex analysis, so you don't understand another comment on the very page you cite, "It is however a diffusion equation in complex space."
No, people are presenting you with the scientific evidence that exists and you are running away to do textual analysis on websites you found with a google search rather than take any time to learn the physics.
Many chemists do more with quantum mechanics that most physicists. You are as ignorant of their activities as you are about physics.
Which nobody denies. We only deny that you have a coherent theory. So far, you have a vague idea reduced to a single .gif and no details that can be compared to scientific observations. And you have a few lies, too.
If you want to cite that effect as evidence for your idea, then you have to show how your idea generates the effect, just like all the scientists mentioned in the wikipedia page did. Somehow, they all managed to predict the effect precisely without the idea that an electron was a bound photon. This being the case, your idea seems entirely superfluous and irrelevant to the experiment.
You can dismiss me as a troll, but that doesn't make your citations any more relevant and it doesn't make your responses any less of a dodge of the real questions.
So you never heard of Count Louis de Broglie? If not, it seems a little inappropriate for you to be "pontificating about physics"
PS by edit: And take a look at the time-independent Schrodinger equation. Where do you think the term $$\frac{\hbar^2}{2m}\equiv \frac{h^2}{8 \pi^2 m}$$ comes from?
Hint: from a rather well-known Danish guy who had what we call a "conjecture".
Go on, for a biscuit take a guess what that conjecture was
Last edited:
Yep. As you will know, "in his 1924 PhD thesis he postulated the wave nature of electrons and suggested that all matter has wave properties". And you will also be aware that the Williamson / van der Mark electron paper was published in Annales de la Fondation Louis de Broglie.
Well I do, so it isn't inappropriate, and I'm not pontificating anyway. I'm just telling you about things you don't know about, and giving you the references to back up what I'm saying.
That the electron in a hydrogen atom is a standing wave. Here's a bit about it. Here's a bit more. And here's a depiction:
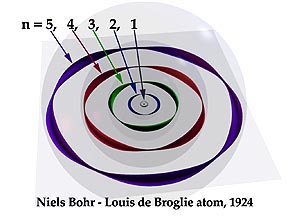
It's a bit simplified, in that the wave isn't actually some twisted little strip, but you catch the drift. Even the atomic orbitals depictions aren't ideal. By the way, standing waves are often thought of as being stationary, but they're not. If you have a standing wave in a cavity like a photon in a mirror-box, then when you drop one of the sides, the photon is off like a shot at c from a standing start. Because it was always moving back and forth at c, even though it looked like it wasn't.
PS: Has anybody seen this Wolf prize?
For "predicting scaling in deep inelastic scattering, leading to identification of nucleon's pointlike constituents"
For point particles!
Aaaaargh!
For "predicting scaling in deep inelastic scattering, leading to identification of nucleon's pointlike constituents"
For point particles!
Aaaaargh!
And yet you continue to assert that the electron does not have "particulate" properties. Weird
No. The Bohr conjecture states that the allowable angular momenta for a bound particle is given by $$\displaystyle n\frac{h}{2 \pi}$$ where $$n$$ is an integer
Putting Bohr and de Broglie in bed together results in the following mental picture, which in my view is more useful than all your images....
If an "orbiting" electron with period $$2 \pi$$, has wave properties, then unless $$n$$ is integer, these waves will interfere destructively with successive "orbits"
Now, no-one buys the idea of "orbits" in this context. And yet a major component of the Schrodinger equation is this conjecture, and the S, eqn. is central to non-relativistic quantum theory.
So, with your knowledge of mathematical physics, for a bonus biscuit, show why the Bohr conjecture written above shows up in the Schrodinger eqn as $$\displaystyle \frac{\hbar^2}{2m}$$.
This is not always true. Usually, you are talking about your own weird ideas, for which you have no references. The wave nature of matter stuff is known, but it also doesn't support your ideas.
OK, can you make a vortex match the information in those references?