Can "Infinity" ever be more than a mathematical abstraction?

[Speakpigeon]

So now the standard is that one has to do something before they can talk about it or it's fuzzy? That's pretty fuzzy logic in and of itself.

Oh you can talk all you like about whatever you like. My point is that there's an obvious flaw in his argument and from the very start. He's started with two massively implausible assumptions without even pausing to recognise as much. That's just very bad logic or very bad rhetoric.
EB

 

[Seattle]

Oh you can talk all you like about whatever you like. My point is that there's an obvious flaw in his argument and from the very start. He's started with two massively implausible assumptions without even pausing to recognise as much. That's just very bad logic or very bad rhetoric.
EB

I haven't watched the video but I know he is also interested in artificial intelligence and his view is that humans don't have to be the only intelligent systems and that machines can be intelligent and they don't have to be so in human ways necessarily.

If you define intelligence in such a way that humans and machines both have those characteristics...so be it.

Machines can already do some things better than humans. He also has another point/view and that is that the goal may not necessarily be to build AI/robots that can fool us as to whether we are interacting with a human or not (the so called Turin test).

We may learn to appreciate such robots for their own uniqueness... maybe kind of like appreciating Spock on Star Trek rather than trying to make him human.

 

[Speakpigeon]

I haven't watched the video but I know he is also interested in artificial intelligence and his view is that humans don't have to be the only intelligent systems and that machines can be intelligent and they don't have to be so in human ways necessarily.
If you define intelligence in such a way that humans and machines both have those characteristics...so be it.
Machines can already do some things better than humans. He also has another point/view and that is that the goal may not necessarily be to build AI/robots that can fool us as to whether we are interacting with a human or not (the so called Turin test).
We may learn to appreciate such robots for their own uniqueness... maybe kind of like appreciating Spock on Star Trek rather than trying to make him human.

Well, Tegmark's assumptions were essentially that an AI within the numerical universe of a video game could be made to somehow have the same sort of understanding of its own numerical universe as we do of our physical one. So Spock doesn't seem to be the best model for that. So, maybe you need to decide what you understand of Tegmark's assumptions. Would a Spock AI be conscious like humans are and feel like humans do? How do you understand Tegmark's assumptions so as to justify his perspective on infinity?
EB

 

[Seattle]

Well, Tegmark's assumptions were essentially that an AI within the numerical universe of a video game could be made to somehow have the same sort of understanding of its own numerical universe as we do of our physical one. So Spock doesn't seem to be the best model for that. So, maybe you need to decide what you understand of Tegmark's assumptions. Would a Spock AI be conscious like humans are and feel like humans do? How do you understand Tegmark's assumptions so as to justify his perspective on infinity?
EB

Tegmark would point out that humans are nothing special but that we just don't know enough yet about how our brains work, it's just chemical reactions and there's nothing special about our "feelings" that machines couldn't adapt as well. You need to define "conscious" but I'm sure you could eventually produce a robot that could meet certain definitions of that.

I don't really know his perspective on infinity because I think in certain cases he is on both sides of that concept.

We tend to think we are "special" but you could define "caring" and then program a robot that, by its actions, was "caring". If you couldn't tell the difference between a machine's "caring" actions and that of a human...then by some definition they are "caring".

 

[mathman]

Even if space is finite in extent, there are an infinite number of possible positions of any object.

 

[someguy1]

I read his book about the mathematical universe. He says he actually believes it and I think I could find places in there where he says that a physical infinity may exist (I can't remember for sure) but I'm also sure I could find other places where he rejects that.

I tried to track this down once and came up with the article I linked, in which he argues for dropping the idea of infinity from physics. If he said the opposite somewhere else, that's interesting.

He does lay out the hypothesis well for the mathematical universe. He does it by bring up Einstein's equivalency principle and by removing "words" thus leaving only the math while giving examples all along the way.

The concept is that something like quarks can be described by only three numbers such as for charge, spin, and type. If we can't see a quark and it can be described by 3 numbers then the quark is essentially just 3 numbers or is equivalent to 3 numbers. If you can't tell the difference between a physical quark and those 3 numbers then they are the same.

I'm not sure I understand that point at all. Is there a difference between the gravitational acceleration of a freefalling body near the earth and the number -32? I'd say there's a huge difference. I can't understand your point here at all. A medical professional could write down all your numbers, your height, weight, blood pressure, and many other technical measurements, but you are not your numbers nor are your numbers you. This argument confuses the map with the territory.

The example used was for gravity and acceleration. You can't tell the difference between the two so they are equivalent.

That's a profoundly different example than a physical phenomenon and its numbers.

Regarding removing "words" and being left only with mathematics, think of chess. There is a chess board, physical pieces, words to describe them but none of that is the essence of "chess". You can eliminate all that and still have chess.

Not really. If I have a recipe for cheesecake, I can't eat that. If a trained chef combines ingredients in a kitchen to make a cheesecake, I can eat that. A musical score is not music. The rules of chess are not the Fischer-Spassky championship match of 1972, or Kasparov versus Deep Blue from 1996. An algorithm is a totally different thing than its execution on actual physical hardware.

Computers do this all the time (computerized chess). The algorithm is "chess".

Not at all. Every programmer knows the difference between a program, which is a list of instructions; and a process, which is the execution of those instructions on physical hardware. You are confusing programs with processes, recipes with food, the rules of chess with a game of chess.

He talks about various types of a multiverse and some require infinity.

That is not true. Physicists often casually use the word "infinity" when they mean "a really big finite number." It's unclear whether multiverse theory requires an actual infinity of universes, or just a whole lot of them.

Black holes and the Big Bang basically require infinity.

I know of no such claim in physics. You're wrong on the facts.

In Quantum Physics the "Many-Worlds" interpretation requires this as well.

No, as noted above. Physicists don't typically mean an actual physically-instantiated infinity.

Here's a heuristic argument to the contrary. If some physical theory (not metaphysical speculation, but an actual theory supported by experiment) claimed there was some actual infinity in the world, wouldn't people ask, is it a countable infinity? Is it uncountable? Is there a cardinal number strictly between this infinity and the set of its subsets, falsifying the continuum hypothesis?

In other words if there's a physical infinity, we must immediately ask, does standard set theory apply to it? Can we do experiments to resolve things like the continuum hypothesis and the axiom of choice? Which of the standard axioms of set theory are literally true about the universe, and which aren't? How about the powerset axiom? How about the axiom of regularity? If there's a physical infinity, all these questions are matters that could in principle be subject to physical experimentation.

The fact that such questions are totally nonexistent in scientific literature shows that nobody takes physical infinity seriously. Rather, when a physicist talks about infinity, they really mean some large finite number.

 

[someguy1]

I like his proposition that the universe does not have "some mathematical properties", but has "only mathematical properties", and that the mathematical properties are surprisingly simple and fundamentally consist of some 33 numerical values (and combinations thereof) and a handful of mathematical equations. He does admit that there are still some missing pieces of the puzzle.

Point being that "the universe is a mathematical structure" is a claim of metaphysics and not physics. I'm certain that Tegmark knows the difference, though his readers often don't.

 

[someguy1]

Even if space is finite in extent, there are an infinite number of possible positions of any object.

Ridiculous. How would you prove such a claim? The Plank scale shows that we can't even sensibly ask the question, let alone answer it. There is a scale of distance below which we cannot measure, and below which we cannot sensibly reason. There is no support in physical science whatsoever for your claim that a physical particle can take take infinitely many distinct positions in space.

And surely you know that all measurement is approximate. Even if you claim that an object could take infinitely many different positions, how would you measure it and thereby prove your claim? No physical apparatus could confirm such a claim.

 

[someguy1]

Yes, I would agree that it's a mistake to make a claim as to the existence of infinities. But, equally, it's a mistake to make any claim as to the inexistence of them. We should just admit that our epistemology is limited and that we just don't know either way.

Yes I agree. My original point was that someday, someone might discover that mathematical infinity is physically meaningful, in the same way that negative numbers, the square root of -1, and non-Euclidean geometry started out as mathematical curiosities and eventually became physically meaningful.

But I feel it's important to push back on the casual use of infinity by physicists when they really mean a large finite number. There are no literal physical infinities in contemporary physics. What the future holds is unknown.

 

[Seattle]

I tried to track this down once and came up with the article I linked, in which he argues for dropping the idea of infinity from physics. If he said the opposite somewhere else, that's interesting.

I'm seen that article and that's why I think he is sometimes on both sides of the issue. In general I think his position is that of the linked paper. In his book (and I may be not be remembering parts of it correctly) I think he tacitly embraces the infinite Universe in some models of inflation while describing his Level 1-4 types of multiverses and when describing certain aspects of Quantum Physics.

Sean Carroll embraces the infinity of Many World's. To your point that physicists are only embracing the math but not the reality...I think that's both true and false. In certain instances they are just using it for the math but in other arguments the argument holds only if they are serious about the physical reality.

I'll try to just hit a few of your other comments by memory. It's true that the Big Bang itself doesn't require a singularity simply because that theory starts just after the singularity and now it generally includes inflation as well. Relativity requires the singularity.

My (limited) understand is that black holes do require infinite space, time, density. If I'm wrong, feel free to point out exactly where I am wrong.

Regarding Max Tegmark's hypothesis on a mathematical universe...I'm not saying that I believe this to be the case. I'm just trying to lay out his hypothesis to the best of my ability and by using some of his examples (chess).

He leads one up to his more complex level 4 Universe with examples that start to get to there. With chess, it's simply to show that if you start with a 3 dimensional chess set, you can replace it on paper with a 2 dimensional version, then you can do away with the physical set altogether by playing computer chess where the rules of the game would not refer to King, Queen, Knights, etc but would simply be algorithms...math with no words or physical equipment required.

This is to set up the scenario which eventually leads to his level 4 multiverse. Again, it is what it is. He is overreaching at this point but it is thought provoking.

 

[Hayden]

No.
Any mathematical entity numbers, even complex numbers, trigonometrical functions, logarithmic functions etc etc are tools to represent, analyse, understand the physical reality.

As such they do not have meaning if they are not associated with any physical entity. 2 may be a real number but stand alone is nothing more than maths, but 2 apples are real.

One of the most interesting example of infinity is black hole singularity, this aspect is purely an outcome of our inability to comprehend beyond event horizon, maths says that in absence of any counter force the entire mass must be compressed to either a point or to a ring of zero thickness, both leading to infinite densities etc, causing problems associated with realism.

 

[Q-reeus]

No.
Any mathematical entity numbers, even complex numbers, trigonometrical functions, logarithmic functions etc etc are tools to represent, analyse, understand the physical reality.

As such they do not have meaning if they are not associated with any physical entity. 2 may be a real number but stand alone is nothing more than maths, but 2 apples are real.

Agreed. A popular counterpart to infinities both large and small, is the notion that 'it's relationships all the way down', i.e. 'it from bit' i.e. physical 'things' as such don't exist. Too much navel gazing and/or pot smoking by certain 'deep thinkers' imo.

One of the most interesting example of infinity is black hole singularity, this aspect is purely an outcome of our inability to comprehend beyond event horizon, maths says that in absence of any counter force the entire mass must be compressed to either a point or to a ring of zero thickness, both leading to infinite densities etc, causing problems associated with realism.

Assumption there is that GR is the correct classical theory of gravity. I'll point you to the same Appendix A at https://arxiv.org/abs/1606.01417 I invited certain others to do.
A very interesting article by Matt Visser et. al. came out recently: https://arxiv.org/abs/1805.03781
I was quite surprised that e.g. Yilmaz exponential metric has a minimum proper radius 'throat' which widens indefinitely as infall progresses. Rather than 'wormhole' though it's better imo to characterize the situation as a vase with a Tardis-like interior proper volume. Main point re infinities being there is never room for a 'singularity' with infinite density even in the unrealistic case of infalling pressureless dust that never fights back against gravity. No need to ever invoke quantized spacetime as rescue mechanism.

 

[someguy1]

I'm seen that article and that's why I think he is sometimes on both sides of the issue. In general I think his position is that of the linked paper. In his book (and I may be not be remembering parts of it correctly) I think he tacitly embraces the infinite Universe in some models of inflation while describing his Level 1-4 types of multiverses and when describing certain aspects of Quantum Physics.

I confess somewhat shamefully that I haven't read his book or his paper; and that my knowledge of the subject is second-hand. I'm setting a summer goal to read his paper. I have the pdf on my computer. I should make an honest man out of myself. The next time I say Tegmark's full of beans, I want to be able to cite chapter and verse. Perhaps my resistance is that I'm secretly worried he'll convert me!

Sean Carroll embraces the infinity of Many World's. To your point that physicists are only embracing the math but not the reality...I think that's both true and false. In certain instances they are just using it for the math but in other arguments the argument holds only if they are serious about the physical reality.

I am not convinced of that latter part but I should go find out because it's central to my thesis. I believe but can not support my understanding that the infinite may be used as a calculating device, as in taking a limit in calculus and using that to make a physical measurement or prediction within the limits of our experimental apparatus and technique. What I do not accept is the ontological reality of the real numbers in the physical universe. Likewise any other infinity that may be used as part of a conceptual argument of some kind, but not to be taken as necessarily real.

I'll take a look at Sean Carroll if he's one who believes in the reality. Because if that's true, someone should ask him about the Continuum hypothesis!

I'll try to just hit a few of your other comments by memory. It's true that the Big Bang itself doesn't require a singularity simply because that theory starts just after the singularity and now it generally includes inflation as well. Relativity requires the singularity.

My understanding of a singularity is this. I know what a mathematical singularity is. It's a point where your function blows up. It's not defined there and it goes to infinity nearby. I do not believe these are literally claimed to exist in physics. There is no physics at the singularity. They can only talk about small neighborhoods around the bad point, but never at the bad point itself. That's math. And to the extent they have an infinity, it's a problem with the theory. But my understanding of singularities in physics is that they are points where we can't say anything sensible. Not that there's "an infinity" sitting there. Do you claim a transfinite ordinal is sitting there? Or what? Mathematicians know all about actual infinities and the physicists just use the word but don't actually mean it, or frankly (IMO) understand it. This I believe. However if I am wrong I REALLY want to hear about this. I don't think I am.

My (limited) understand is that black holes do require infinite space, time, density. If I'm wrong, feel free to point out exactly where I am wrong.

My understanding is that at the bad points we just say, "We don't know. There's no physics there." And NOT, "there's a set there like Cantor thought of, and it has infinitely many of something, or infinitely much energy or charge or whatever." We do NOT SAY THAT. I do not personally believe there is a physicist alive who, after spending five minutes with a professional set theorist who knows some physics, would not back down on their claim of actual infinity.

I'm quite convinced of this. I really need to see some specific links to counterexamples so that I can understand and either refute or accept them.

Regarding Max Tegmark's hypothesis on a mathematical universe...I'm not saying that I believe this to be the case. I'm just trying to lay out his hypothesis to the best of my ability and by using some of his examples (chess).

I appreciate it. I should really go read Tegmark so I have some idea what I'm actually talking about.

He leads one up to his more complex level 4 Universe with examples that start to get to there. With chess, it's simply to show that if you start with a 3 dimensional chess set, you can replace it on paper with a 2 dimensional version, then you can do away with the physical set altogether by playing computer chess where the rules of the game would not refer to King, Queen, Knights, etc but would simply be algorithms...math with no words or physical equipment required.

I think I'm getting the idea that everything can be abstracted and is in its essence non-physical. That the real world lives in bitstring space (MUH) or computable bitstring space (CUH). That because we humans have the power of abstraction, the world must be abstract. But then what's all this stuff around us? I really need to go read that book and/or paper. I want to understand why a serious person is saying these things.

If I recall, Scott Aaronson (computer scientist and blogger) says Tegmark's interesting but that his thesis is ultimately meaningless. I seem to recall reading him to that effect. I'll double check.

This is to set up the scenario which eventually leads to his level 4 multiverse. Again, it is what it is. He is overreaching at this point but it is thought provoking.

Yes I agree. I should either go read his paper or else stop thinking I know what he's talking about.

Thanks for the insights.

 

[Speakpigeon]

Tegmark would point out that humans are nothing special but that we just don't know enough yet about how our brains work, it's just chemical reactions and there's nothing special about our "feelings" that machines couldn't adapt as well. You need to define "conscious" but I'm sure you could eventually produce a robot that could meet certain definitions of that.
I don't really know his perspective on infinity because I think in certain cases he is on both sides of that concept.
We tend to think we are "special" but you could define "caring" and then program a robot that, by its actions, was "caring". If you couldn't tell the difference between a machine's "caring" actions and that of a human...then by some definition they are "caring".

If humans are nothing special, and I'm prepared for the day when this is properly demonstrated, then I would expect machines to have subjective experience and experience qualia, too. And then, pretty much anything from the whole universe itself down to bacterium and to quarks should also somehow experience qualia. Qualia would have to be part and parcel of the physical world. And then, of course, this puts a spanner in Tegmark's work because I fail to see how qualia, i.e. qualities, would now be in fact numbers, i.e. quantities. There would have to be a lot of explaining to do.
Second, one essential way that humans seem to model the physical world is by assuming it's ontological nature. Ontology is not some deranged metaphysician's dream, it's inherent in our mental representation of the physical world. We even have a marked tendency to reify all sorts of abstract ideas like Good and Evil, and now mathematical concepts, etc. This is of course debatable, but what we cannot do, short of madness, is convince ourselves that the world out there somehow doesn't exist as an independent reality. And we also believe we are to some extent subjected to its laws. So, what about AI machines? Would they end up adopting a similar bias in their representation of the world? If we're not special, some of them at least should end up doing the same thing, too. And the AI within the video game could do it as well, and come to reify its digital environment as if it was an ontological reality, rather than a transient and contingent part of a larger universe. But if machines are like us, then we are like machines. And then, how are we going to be able to tell what is the reality of things? As I see it, the world makes sense to us because we've persisted through our own very long evolution within it. We couldn't survive in it as human beings without some ability to make sense of it. If we dismiss our natural ability, we'll need some alternative. And I don't trust that people like Tegmark or anyone could even conceive of any such alternative. I don't even buy that he could possibly really believe his own stories. It's one thing to offer challenging ideas, it's another to really believe them. Why would you even do anything at all if you didn't truly believe the world around you is absolutely exactly as it looks and even smell and feels to you? Ask people with mental disorders whereby reality suddenly seems really weird and even unreal. I don't think you would enjoy it at all. So, great ideas, challenging ideas, but to take with a pinch of salt. Perhaps Tegmark would need to explain how he sees the usefulness of his ideas. Me, I don't think we want to go there.
EB

 

[Seattle]

No.
Any mathematical entity numbers, even complex numbers, trigonometrical functions, logarithmic functions etc etc are tools to represent, analyse, understand the physical reality.

As such they do not have meaning if they are not associated with any physical entity. 2 may be a real number but stand alone is nothing more than maths, but 2 apples are real.

One of the most interesting example of infinity is black hole singularity, this aspect is purely an outcome of our inability to comprehend beyond event horizon, maths says that in absence of any counter force the entire mass must be compressed to either a point or to a ring of zero thickness, both leading to infinite densities etc, causing problems associated with realism.

How would you describe a quark?

If humans are nothing special, and I'm prepared for the day when this is properly demonstrated, then I would expect machines to have subjective experience and experience qualia, too. And then, pretty much anything from the whole universe itself down to bacterium and to quarks should also somehow experience qualia. Qualia would have to be part and parcel of the physical world. And then, of course, this puts a spanner in Tegmark's work because I fail to see how qualia, i.e. qualities, would now be in fact numbers, i.e. quantities. There would have to be a lot of explaining to do.
Second, one essential way that humans seem to model the physical world is by assuming it's ontological nature. Ontology is not some deranged metaphysician's dream, it's inherent in our mental representation of the physical world. We even have a marked tendency to reify all sorts of abstract ideas like Good and Evil, and now mathematical concepts, etc. This is of course debatable, but what we cannot do, short of madness, is convince ourselves that the world out there somehow doesn't exist as an independent reality. And we also believe we are to some extent subjected to its laws. So, what about AI machines? Would they end up adopting a similar bias in their representation of the world? If we're not special, some of them at least should end up doing the same thing, too. And the AI within the video game could do it as well, and come to reify its digital environment as if it was an ontological reality, rather than a transient and contingent part of a larger universe. But if machines are like us, then we are like machines. And then, how are we going to be able to tell what is the reality of things? As I see it, the world makes sense to us because we've persisted through our own very long evolution within it. We couldn't survive in it as human beings without some ability to make sense of it. If we dismiss our natural ability, we'll need some alternative. And I don't trust that people like Tegmark or anyone could even conceive of any such alternative. I don't even buy that he could possibly really believe his own stories. It's one thing to offer challenging ideas, it's another to really believe them. Why would you even do anything at all if you didn't truly believe the world around you is absolutely exactly as it looks and even smell and feels to you? Ask people with mental disorders whereby reality suddenly seems really weird and even unreal. I don't think you would enjoy it at all. So, great ideas, challenging ideas, but to take with a pinch of salt. Perhaps Tegmark would need to explain how he sees the usefulness of his ideas. Me, I don't think we want to go there.
EB

He sees the usefulness of his mathematical universe idea in that "if" the important questions are actually mathematical in nature then all important questions may, some day, be answerable.

We may not be able to go to another universe but we may be able to answer questions about another universe if it's accurately modeled by mathematics. If it's not, then there will be some unanswerable questions. This is why his hypothesis has appeal for him.

Regarding your reality comments. I'll just say that he distinguishes between our internal realities, our external realities and consensus external realities. I think most people would agree with those distinctions. Meaning that we can shut our eyes and still have thoughts, open our eyes and perceive that someone suddenly running into the room is aggressive and yet the consensus opinion of most people in that room may be that the runner wasn't particularly aggressive.

 

[Write4U]

Point being that "the universe is a mathematical structure" is a claim of metaphysics and not physics. I'm certain that Tegmark knows the difference, though his readers often don't.

If the universe is a geometric object, then it is by definition a mathematical object, no?

Even a manifold or a toroid would have only mathematical geometric properties.

This is why we can name them in the first place. They can be measured and represented with mathematical symbols.

It really makes no difference which genre (specific type) of mathematics one uses to symbolize a dimensional universe. As long as the calculus yields the same relative results, it's still mathematical, no?

I am sure Tegmark does not believe the number 2 is a physical object, it represents the value of an object, usually accompanied by a physical characteristic. 2 Meters, 2 Joules, 2 Hz, etc

Can one represent a metaphysical object at all?

 

[someguy1]

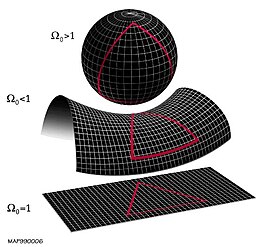
If the universe is a geometric object, then it is by definition a mathematical object, no?

Of course. But you are confusing the map with the territory. I perfectly well agree that math is "unreasonably effective" in the physical sciences. The claim that the universe IS the math is a claim of metaphysics.

From the standpoint of someone who's studied more math than physics, my understanding is that mathematicians don't care in general whether their work is "real". Their work has value purely as abstraction. No connection with reality is ever implied when it comes to math. Math only tells you what's logically true based on the axioms ... and we don't even know for sure that our axioms are consistent!

So math is more like chess, a game with formal rules that's fun to play. We wouldn't say, "The universe is a game of chess and we're the pieces." That would be taken as stoner philosophy, agree?

But Tegmark says, "The universe is math," just because certain aspects of the universe can be described to a given degree of approximation subject to the limitations of the experimental or observational apparatus and technique. Confusing map with territory. And believing one's maps and models are real, as opposed to our own mind's interpretation of what's real. Math may be "out there," but it's also "in here," coded in our brains at a very low level. Wouldn't you like to know why it is that the human brain can do math at all? Tegmark's not asking the hard questions.

To imagine mathematics is exact in its description of reality is to commit a grave fallacy of the philosophy of science. And then to believe the math "is" rather than models the world ... that's just wrong.

I hope you don't mind if I don't engage with the rest of your post, although I enjoyed your diagram.


I actually dropped in to mention that I confirmed Aaronson's negative impression (not of the book, which everyone agrees is stimulating and educational regardless of whether you believe in his ultimate thesis.

But I did want to pass on this one quote from Peter Woyt, who writes the great physics blog Not Even Wrong.

Tegmark’s career is a rather unusual story, mixing reputable science with an increasingly strong taste for grandiose nonsense. In this book he indulges his inner crank, describing in detail an uttery empty vision of the “ultimate nature of reality.” What’s perhaps most remarkable about the book is the respectful reception it seems to be getting

There's plenty more where that came from. Woit's review is here, http://www.math.columbia.edu/~woit/wordpress/?p=6551.

And Aaronson's review is here: https://www.scottaaronson.com/blog/?p=1753

I probably won't read the book. But I am actually planning to make a run at reading his original paper. I have the pdf and it's not that overly long and I can probably get a better sense of his terminology and ideas. I'm sure I'll learn a lot from studying his work.

But on the metaphysics, it seems laughably wrong to be. Mathematical structures are very abstract. And in fact one of the criticisms is that he doesn't actually spend much time talking about the actual math. I get the feeling that "math" for Tegmark is "the equations that physicists use," and not math as actually practiced by mathematicians.

I have studied a fair number of those abstract entities that go by the name of "mathematical structures." And believe me, the universe isn't one of those. Not unless you believe that the universe is an artifact of set theory. Or you're arguing some sort of structuralist position that the structures are independent of our representations of them. Tegmark understands none of this as far as I know.

So anyway I think it's unfortunate if the interesting discussion of whether infinity might be actually instantiated in the physical world got sidetracked into what Tegmark thinks. That's another criticism of Tegmark. That his brand of pop metaphysics wrapped up in scientism crowds out intelligent discussion of the fundamentals.

I'm not going to talk about Tegmark anymore. But I am going to make a serious run at his paper, which by the way is here if anyone's interested. https://arxiv.org/pdf/0704.0646.pdf

Ok thanks for listening. No more Tegmark rants from me but I would love to talk about what it means for actual infinity to be instantiated in the world. And I'd welcome specific pointers to claims that actual infinity is instantiated in some theory. Sean Carroll's Wiki page didn't say anything about it.

 

[Q-reeus]

Seems nobody bothered to watch that YT vid of George Ellis's great lecture linked to in #4. Just maybe would have saved a lot of redundant and long posts here. Maybe.

 

[someguy1]

Seems nobody bothered to watch that YT vid of George Ellis's great lecture linked to in #4. Just maybe would have saved a lot of redundant and long posts here. Maybe.

Looks like he's addressing my questions. I'll watch it.

ps (about 2 minutes later):

Well I am sorry but I got to my first howler at only 1:41, that didn't take very long. He said that infinity is not a number and is something that can "never be attained."

Now he is entitled to his opinion, but he is expressing the idea of the "potential" infinity from the days of Aristotle.

However today mathematicians have a very advanced theory of tranfinite numbers that began with Georg Cantor's work in the 1870's. So Professor Ellis, eminent and learned as he may be, is either ignorant or rejects all of mathematics developed in the last 140 years. And you could not do modern physics without the mathematical theory of infinity.

If he corrects this error or puts it into a more modern mathematical context later, please let me know and I'll continue watching. Otherwise sorry, no sale.

ps -- I skimmed through the rest of it. It looks like a fairly conventional overview of well-known ideas. I did not stick around to see his specific examples. Frankly I was turned off by his starting with the wrong definition and understanding of infinity, as if the past 140 years of mathematics didn't happen.

pps -- Ok I skimmed some more, he gets to the measurement problem and related topics. So there is some point in this 47 minute video which is the part I want to see. I'll try to find it. I can see there's a pony in there somewhere.

 

[Q-reeus]

Looks like he's addressing my questions. I'll watch it.

ps (about 2 minutes later):

Well I am sorry but I got to my first howler at only 1:41, that didn't take very long. He said that infinity is not a number and is something that can "never be attained."

Now he is entitled to his opinion, but he is expressing the idea of the "potential" infinity from the days of Aristotle.

However today mathematicians have a very advanced theory of tranfinite numbers that began with Georg Cantor's work in the 1870's. So Professor Ellis, eminent and learned as he may be, is either ignorant or rejects all of mathematics developed in the last 140 years. And you could not do modern physics without the mathematical theory of infinity.

If he corrects this error or puts it into a more modern mathematical context later, please let me know and I'll continue watching. Otherwise sorry, no sale.

ps -- I skimmed through the rest of it. It looks like a fairly conventional overview of well-known ideas. I did not stick around to see his specific examples. Frankly I was turned off by his starting with the wrong definition and understanding of infinity, as if the past 140 years of mathematics didn't happen.

pps -- Ok I skimmed some more, he gets to the measurement problem and related topics. So there is some point in this 47 minute video which is the part I want to see. I'll try to find it. I can see there's a pony in there somewhere.

I really suggest you take the time to watch at least all of part 1 lecture. The physical unattainability of infinity is labored somewhat to begin with. But how that fits into infinities as applied to cosmology where actual infinity is often assumed wrt size of our universe, and then to multiverse concepts, is very sound imo. The followup Q & A to part 1 is also good. Part 2 gets technical in places but has a nice roundup at the end - a triumph of common sense if you like. Anyway your choice.