Black holes and the relativity of simultaneity

[Schmelzer]

Are you working on stuff that isn't ether related? Just curious.

Actually I think more about interpretations of quantum theory.

I clearly favor interpretations which have trajectories, like de Broglie-Bohm theory, which uses a trajectory $$q(t)$$ and a wave function $$\psi(q,t)$$ for the description of reality. There are two things which are often criticized: First, that the trajectories of dBB theory are sometimes surrealistic. I think about the possibility of hidden trajectories in the phase space, thus, $$q(t), p(t)$$, which may be less surrealistic. In fact this is a quite weak objection, why would one wonder that quantum trajectories look strange, but, nonetheless, why not think about possibilities to improve a theory.

The other weak place is the role of the wave function $$\psi(q,t)$$. The question is if it can be interpreted similar to a probability, as describing only insufficient human knowledge (epistemic), or if it defines some element of reality, something really existing (ontic). I think, it should be possible to interpret the wave function as epistemic. Or, more accurate, the wave function of the whole (system + preparation measurement device) would be epistemic, while the effective wave function of the system would include information of the state of the preparation measurement device, and, therefore, contain ontic elements.

 

[sweetpea]

In GR (that means, if GR would be true) they would exist in reality. There are some subtleties in their definition (the definition of a horizon depends on the global solution, not on what exists now), and there is no known quantization of GR, while it is known that gravity has to be quantized. But in classial GR, such horizons exist.

I can understand where your coming from with the global solution if you mean the global Schwarzschild solution ? Perhaps, I should say, using Schwarzschild coordinates would allow for a disant global view of a black hole?

If there is a meaningful global notion of "now", it requires more than defined by GR, because it requires some global contemporaneity. The "now" one light-year away should be only a "now", even a whole second would be too long for a "now", while "spacelike separates" would define there only a whole two years long history instead of a "now".

So, if we were to leave our very distant view of a black hole, that is, leave our Schwarzschild global view, and start to approach the horizon, what would we find at the horizon which we didn't or couldn't record from our distant global view? Would this horizon "now" be reachable? And even crossable? Even noticable? I know this may all seem obvious because we have changed frame from distant view to 'in faller'.

 

[krash661]

because you are mistaken on this point.

says the unqualified, inexperienced want-to-be intellect.
(shakes head) it is remarks exact to this that are made by average individuals whom do nothing but click on wkki or some other links, and now believes they are some sort of science genius, that destroy these science sites..

 

[Schmelzer]

I can understand where your coming from with the global solution if you mean the global Schwarzschild solution ? Perhaps, I should say, using Schwarzschild coordinates would allow for a disant global view of a black hole?

No. In the GR spacetime interpretation, what exists is the whole spacetime. The block universe. There is no "now" which exists and a future which does not yet exist. Our future already exists, in the same way as our now exists.

And, of course, following the GR spacetime interpretation, you can reach the part behind the horizon, whenever you decide to do this (as part of a decision for suicide), if you are close enough to a BH. You reach it in finite proper time, which can be computed. If the BH is big enough, you can cross the horizon without being destroyed by tidal forces.

According to classical GR. But I would not recommend you to bet that this theory remains valid near the horizon.

 

[sweetpea]

No. In the GR spacetime interpretation, what exists is the whole spacetime. The block universe. There is no "now" which exists and a future which does not yet exist. Our future already exists, in the same way as our now exists. And, of course, following the GR spacetime interpretation, you can reach the part behind the horizon, whenever you decide to do this (as part of a decision for suicide), if you are close enough to a BH. You reach it in finite proper time, which can be computed. If the BH is big enough, you can cross the horizon without being destroyed by tidal forces.
According to classical GR. But I would not recommend you to bet that this theory remains valid near the horizon.

Maybe I didn't explain myself clearly. To cut a long story short... I was trying to show how the horizon is just a coordinate singularity (CS), that is, a CS which only shows in the Schwarzschild coordinates used by the distant observer. For the in-faller this CS doesn't appear.

I will try to find an old link to where a Prof: Don Koks describes how at the horizon nothing unusual is happing and that spacetime is normal there, and he shows this without even using Kruska-Szekeres coordinates. Maybe that's what you are saying. I have to check-out google books for this link.
I see the point about there being no universal now in GR.

 

[RJBeery]

...the wave function of the whole (system + preparation measurement device) would be epistemic, while the effective wave function of the system would include information of the state of the preparation measurement device, and, therefore, contain ontic elements.

If you're in for a penny granting ontic elements to a measurement device (where the measurement ostensibly takes place in our causal future) why not be in for a pound and reject the wavefunction completely? This is precisely what the block universe is.

 

[brucep]

I can understand where your coming from with the global solution if you mean the global Schwarzschild solution ? Perhaps, I should say, using Schwarzschild coordinates would allow for a disant global view of a black hole?



So, if we were to leave our very distant view of a black hole, that is, leave our Schwarzschild global view, and start to approach the horizon, what would we find at the horizon which we didn't or couldn't record from our distant global view? Would this horizon "now" be reachable? And even crossable? Even noticable? I know this may all seem obvious because we have changed frame from distant view to 'in faller'.

r_s is a coordinate singularity as a result of the radial stretching component being singular at r=2M. When you integrate this over the path the coordinate singularity disappears and in its place is a formula which reveals the distance to 2M is finite. Real coordinates where the spacetime curvature isn't infinite. That was one of the first things I learned while reading my first text. The only folks who freak out over singular coordinates seem to be cranks who want to deny the existence of black holes.

 

[danshawen]

Let's start over because I started confusing things with spacelike separation references. I'm certain that Schmelzer and I (and I hope everyone else) agree that timelike separated events are well ordered and not up for interpretation. It's simply a mathematical fact that the creation and growth of a black hole exists in nobody's past light cones. This is true of all observers AND all observers making judgments about all other observers (which is why I confusingly brought in the spacelike separation issue). Look at the light cones of every point (i.e. potential observers) in this diagram. You can see, visually, that the past light cones tilt to perfectly coincide with the creation of the event horizon.

If a persistent object A, such as a black hole, is said to coexist with us as observers then we would expect a time to pass such that A's history comes into our past light cone. In other words, the event horizon exists for us today even less than Christmas Day 2100, because Christmas Day 2100 will enter our past light cones eventually.

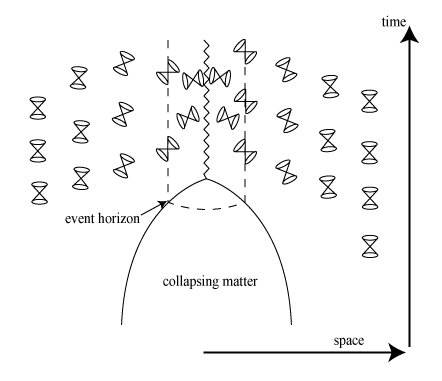
Nice diagram! The illustration is a quarter section sliver of a black hole event horizon, and various light cones for different observers some distance from where the EH has formed.

This illustrates exactly the point I was trying to make about light cones and event horizons. If light is bending around a black hole (without being captured in its event horizon, obviously, some observers somewhere will be able to notice those in their "world lines" against the edges of the cones defined by the propagation of light reaching them from the vicinity of the black hole.

I understand that for as long as the black hole persists temporally, eventually light from near it (or skirting the black hole) can reach almost any point in the known universe, subject only to constraints imposed by the speed of light and the location of the BH.

In this respect, the black hole is no different from a black box. The only way we could be assured of detecting its presence would be by means of a partial eclipse (it would hide or gravitationally lens the stars and galaxies behind it until they cleared the field).

This tells us exactly nothing about what is going on inside of the EH, and the light cones don't really help the model conceptually either. Time dilates in the vicinity of the BH gravitational field, which is the reason light appears to bend around it.

As to whether or not the light cones "really" extend into "the past" where the black hole collapsed, this has no real meaning for light cones anyway. In Minkowski's universe, time was still an absolute, anchored to covariant remnants of a geometry of absolute space by means of the Pythagorean theorem, complex numbers, and invariant 4D "intervals" for vectors in 4D spacetime. Vectors in relativistic space don't add like vectors in the Euclidean geometry of solids that never move. Space doesn't "warp" like a 4D version of a 2D rubber sheet because there is no inertia nor absolute origin anchored in space comprised of three dimensions of inertialess light travel time. The only vector geometrical relationship that works in relativistic space is to add +c to -c in diametrically opposite directions to obtain exactly what "at rest", or v=zero means, for any inertial reference frame. Minkowski's simultaneity was not the same simultaneity we understand derives of quantum entanglement. And none of the relationships he put forward to explain simultaneity in relativity make any sense for REAL simultaneity that derives of entanglement, because this simultaneity even outruns the speed of light.

Calculating 4D intervals to determine the 4D distance vectors between quantum entangled events (faster than c) makes exactly no sense at all, in any version of the math Minkowski proposed, yet this is EXACTLY what he meant by the term "simultaneity" in relativity. I can't make the argument against using light cones or anything else Minkowski proposed any stronger than that. It isn't likely to provide insight into the goings on inside of a BH, at any rate.

Physicsforums has a lively discussion of this:

https://www.physicsforums.com/threa...lement-and-relativity-of-simultaneity.633942/

And I have adopted no point of view expressed there. The respective languages of QM and relativity are both sorely in need of a revision that makes them consistent with each other. Dropping Minkowski's 4D spacetime altogether is the quickest way I can see to resolve the problem. You don't need Lorentz covariance, 4D intervals, Minkowski rotation, spacetime warpage, or light cones. Time dilation and relativity all by itself works just fine to describe the dynamics of quantum entanglement and bulk energy propagation in three dimensions, all of which are light travel time.

 

[Schmelzer]

If you're in for a penny granting ontic elements to a measurement device (where the measurement ostensibly takes place in our causal future) why not be in for a pound and reject the wavefunction completely? This is precisely what the block universe is.

I don't understand. To grant the measurement device an ontic status is natural and unproblematic. The Copenhagen interpretation grants this too - as part of the classical world. This has nothing to do with what happens in the future. One can assign all the potential measurement devices which exist now an ontic status, without assigning their future states an ontic status now.

I see some change to give the full wave function an epistemic status, so that only the reduced, effective wave function $$\psi_{sys}(q_{sys},t) = \psi_{full}(q){sys}, q_{meas}(t),t)$$ obtains ontic status because of its dependence on an ontic object, the measurement device [te]q_{meas}(t)[/tex]. The block universe is something I reject, I see also no compatibility with the probabilistic character of quantum theory.

 

[Schmelzer]

Ups, the formulas should look like:

$$\psi_{sys}(q_{sys},t) = \psi_{full}(q_{sys}, q_{meas}(t),t)$$

$$q_{meas}(t)$$.

 

[danshawen]

The block universe is something I reject, I see also no compatibility with the probabilistic character of quantum theory.

I would agree.

"Block" universes are ones in which conservation of energy does not apply, because a snapshot of the universe taken in an instant of time (delta t equals zero) means, the propagation of energy has stopped. This never happens in the real universe, other than for energy that is 100% bound AND ALSO is at rest. The bound energy that is matter at rest is the only kind of "persistence" with respect to an instant of time which satisfies conservation of energy, and even that state is very dynamic, not really like a "snapshot".

Multiverses likewise are an affront to conservation of energy, making perpetual motion machines powered by energy derived from other universes or the vacuum energy of space possible. All signs in this universe point in the direction of the interaction with fields in the vacuum being intimately responsible for the law of conservation of energy.

The whole idea of multiverses, like its predecessor polytheism, need to die an ignoble death, and block universes can be retired to the same recycling bin. Each decision made in this universe does not instantiate an alternate version of the universe, because the quantity of energy used to create another universe at each instant would not be conserved. Where would the energy to create so many other universes come from? You'd need a theory to cover multiple instances of both inflation and the Big Bang from the instant of creation also, wouldn't you?

Physicists and mathematicians who continue to support Block universes and Multiverses need to go back to writing fiction.

 

[RJBeery]

I don't understand. To grant the measurement device an ontic status is natural and unproblematic. The Copenhagen interpretation grants this too - as part of the classical world. This has nothing to do with what happens in the future. One can assign all the potential measurement devices which exist now an ontic status, without assigning their future states an ontic status now.

I see some change to give the full wave function an epistemic status, so that only the reduced, effective wave function $$\psi_{sys}(q_{sys},t) = \psi_{full}(q){sys}, q_{meas}(t),t)$$ obtains ontic status because of its dependence on an ontic object, the measurement device [te]q_{meas}(t)[/tex]. The block universe is something I reject, I see also no compatibility with the probabilistic character of quantum theory.

So you tend towards a "wave function collapse" interpretation, correct?

 

[RJBeery]

Multiverses likewise are an affront to conservation of energy, making perpetual motion machines powered by energy derived from other universes or the vacuum energy of space possible. All signs in this universe point in the direction of the interaction with fields in the vacuum being intimately responsible for the law of conservation of energy.

The whole idea of multiverses, like its predecessor polytheism, need to die an ignoble death, and block universes can be retired to the same recycling bin. Each decision made in this universe does not instantiate an alternate version of the universe, because the quantity of energy used to create another universe at each instant would not be conserved. Where would the energy to create so many other universes come from? You'd need a theory to cover multiple instances of both inflation and the Big Bang from the instant of creation also, wouldn't you?

Physicists and mathematicians who continue to support Block universes and Multiverses need to go back to writing fiction.

I completely agree that "multiverses" are extremely problematic. While I can't do it right now I'll try to show you and Schmelzer why wave function collapse leads directly to a block universe (which is my preferred interpretation). Perhaps this should be done under a new thread?

 

[Schmelzer]

So you tend towards a "wave function collapse" interpretation, correct?

Not. In de Broglie-Bohm theory we have no collapse of the global wave function. We have only a collapse of effective wave functions of subsystems.

 

[sweetpea]

r_s is a coordinate singularity as a result of the radial stretching component being singular at r=2M. When you integrate this over the path the coordinate singularity disappears and in its place is a formula which reveals the distance to 2M is finite. Real coordinates where the spacetime curvature isn't infinite. That was one of the first things I learned while reading my first text. The only folks who freak out over singular coordinates seem to be cranks who want to deny the existence of black holes.

Yes bruce, that formula is on page 2-49 of EBH. I was going to make a link to Don kok's book, to show how he goes about showing space-time is normal at the horizon and he shows this without using Kruskal-Szekeres coordinates. But, because of 'restricted pages' on google books, it would be a messy two links to get- around those restricted pages so as to show the three pages of interest. But I don't think it's worth my time on this thread, when you remember the habit of this threads originator in his OPs.
remember this OP...

With respect...all of you non-critical thinkers can kiss my a$$.

Besides, I have two people on this thread on ignore and it's like snow blindness looking at this thread

 

[RJBeery]

I don't remember writing that but if you were offended perhaps you self-identified.

 

[brucep]

Yes bruce, that formula is on page 2-49 of EBH. I was going to make a link to Don kok's book, to show how he goes about showing space-time is normal at the horizon and he shows this without using Kruskal-Szekeres coordinates. But, because of 'restricted pages' on google books, it would be a messy two links to get- around those restricted pages so as to show the three pages of interest. But I don't think it's worth my time on this thread, when you remember the habit of this threads originator in his OPs.
remember this OP...Besides, I have two people on this thread on ignore and it's like snow blindness looking at this thread

I'm in that mode to much. Don Kok's book. He uses the remote bookkeeper spacetime and substitutes the integral for the radial stretching component as the bases of his analysis? I'll find it to see what he actually does. Thank's.
Explorations in Mathematical Physics. I should read that.