Back onto some professional science and professional scientists and their research.....in this case Professor Sean Carroll.......
http://www.preposterousuniverse.com/blog/2016/07/18/space-emerging-from-quantum-mechanics/
Space Emerging from Quantum Mechanics
Posted on July 18, 2016 by Sean Carroll
The other day I was amused to find
a quote from Einstein, in 1936, about how hard it would be to quantize gravity: “like an attempt to breathe in empty space.” Eight decades later, I think we can still agree that it’s hard.
So here is a possibility worth considering: rather than quantizing gravity, maybe we should try to gravitize quantum mechanics. Or, more accurately but less evocatively, “find gravity inside quantum mechanics.” Rather than starting with some essentially classical view of gravity and “quantizing” it, we might imagine starting with a quantum view of reality from the start, and find the ordinary three-dimensional space in which we live somehow emerging from quantum information. That’s the project that ChunJun (Charles) Cao, Spyridon (Spiros) Michalakis, and I take a few tentative steps toward in
a new paper.
We human beings, even those who have been studying quantum mechanics for a long time, still think in terms of a classical concepts. Positions, momenta, particles, fields, space itself. Quantum mechanics tells a different story. The quantum state of the universe is not a collection of things distributed through space, but something called a
wave function. The wave function gives us a way of calculating the outcomes of measurements: whenever we measure an observable quantity like the position or momentum or spin of a particle, the wave function has a value for every possible outcome, and the probability of obtaining that outcome is given by the wave function squared. Indeed, that’s typically how we construct wave functions in practice. Start with some classical-sounding notion like “the position of a particle” or “the amplitude of a field,” and to each possible value we attach a complex number. That complex number, squared, gives us the probability of observing the system with that observed value.
Mathematically, wave functions are elements of a mathematical structure called
Hilbert space. That means they are vectors — we can add quantum states together (the origin of
superpositions in quantum mechanics) and calculate the angle (“dot product”) between them. (We’re skipping over some technicalities here, especially regarding complex numbers — see e.g.
The Theoretical Minimum for more.) The word “space” in “Hilbert space” doesn’t mean the good old three-dimensional space we walk through every day, or even the four-dimensional spacetime of relativity. It’s just math-speak for “a collection of things,” in this case “possible quantum states of the universe.”
Hilbert space is quite an abstract thing, which can seem at times pretty removed from the tangible phenomena of our everyday lives. This leads
some people to wonder whether we need to supplement ordinary quantum mechanics by additional new variables, or alternatively to imagine that wave functions reflect our knowledge of the world, rather than being representations of reality. For purposes of this post I’ll take the
straightforward view that quantum mechanics says that the real world is best described by a wave function, an element of Hilbert space, evolving through time. (Of course time could be emergent too … something for another day.)
Here’s the thing: we can construct a Hilbert space by starting with a classical idea like “all possible positions of a particle” and attaching a complex number to each value, obtaining a wave function. All the conceivable wave functions of that form constitute the Hilbert space we’re interested in. But we don’t
have to do it that way. As Einstein might have said, God doesn’t do it that way. Once we make wave functions by quantizing some classical system, we have states that live in Hilbert space. At this point it essentially doesn’t matter where we came from; now we’re in Hilbert space and we’ve left our classical starting point behind. Indeed, it’s well-known that very different classical theories lead to the same theory when we quantize them, and likewise some quantum theories don’t have classical predecessors at all.
The real world simply is quantum-mechanical from the start; it’s not a quantization of some classical system. The universe is described by an element of Hilbert space. All of our usual classical notions should be derived from that, not the other way around. Even space itself. We think of the space through which we move as one of the most basic and irreducible constituents of the real world, but it might be better thought of as
an approximate notion that emerges at large distances and low energies.
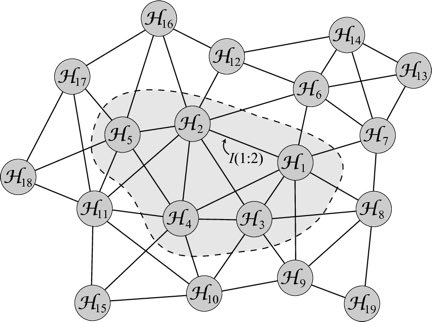
So here is the task we set for ourselves: start with a quantum state in Hilbert space. Not a random or generic state, admittedly; a particular kind of state. Divide Hilbert space up into pieces — technically, factors that we multiply together to make the whole space. Use quantum information — in particular, the amount of
entanglement between different parts of the state, as measured by the
mutual information — to define a “distance” between them. Parts that are highly entangled are considered to be nearby, while unentangled parts are far away. This gives us a graph, in which vertices are the different parts of Hilbert space, and the edges are weighted by the emergent distance between them.
We can then ask two questions:
- When we zoom out, does the graph take on the geometry of a smooth, flat space with a fixed number of dimensions? (Answer: yes, when we put in the right kind of state to start with.)
- If we perturb the state a little bit, how does the emergent geometry change? (Answer: space curves in response to emergent mass/energy, in a way reminiscent of Einstein’s equation in general relativity.)
It’s that last bit that is most exciting, but also most speculative. The claim, in its most dramatic-sounding form, is that gravity (spacetime curvature caused by energy/momentum) isn’t hard to obtain in quantum mechanics — it’s automatic! Or at least, the most natural thing to expect. If geometry is defined by entanglement and quantum information, then perturbing the state (e.g. by adding energy) naturally changes that geometry. And if the model matches onto an emergent field theory at large distances, the most natural relationship between energy and curvature is given by Einstein’s equation. The optimistic view is that gravity just pops out effortlessly in the classical limit of an appropriate quantum system. But the devil is in the details, and there’s a long way to go before we can declare victory.