Galileo was technically WRONG

[RJBeery]

Umm, but you know where it came from because you replied to it. I'm trying to bring Fednis over to this proper thread.

 

[OnlyMe]

This whole issue is addressed by, The force of gravity is the same for atoms and baseballs

 

[exchemist]

Except that while the earth is pulled up toward the bowling ball shortening the distance.., in the case of the golf ball, IT (the golf ball) falls toward the earth faster than the bowling ball does.., also shortening the distance...

This is never an issue, if you always use the earth as the frame of reference for the fall in both cases.., because all of the closing velocity is then attributed to the smaller object. When you try to look at it from the rest frame before the drop you have to take into account that the golf ball falls faster toward the earth than the bowling ball does.., which is exactly balanced by the difference in how fast the earth falls toward the smaller object in each case.

You are wrong! And as been pointed out Newton and Einstein are both right. Take the time to look over, The force of gravity is the same for atoms and baseballs. That should be a larger difference in mass than your bowling and base ball fantasy. And I am sure than even though I don't want to strain myself with the math, the researchers involved had no issue with the math... Without a reference I think I also remember a proposed test with neutrons, but I am unsure and a little skeptical given the short half life of a free neutron.

This is what I thought too, though I confess the more I thought about it the less confident I became! Beery's diagram makes the problem look clearer. I think we can settle this by means of looking at the maths for the two cases, i.e. one case in which the larger mass is taken as the frame of reference to describe the motions and the other in which the frame is that of the masses before release. Maybe in the morning my head will be clear enough - or maybe someone good at Newtonian dynamics can have a go in the meantime. It should be fairly straight forward.

 

[RJBeery]

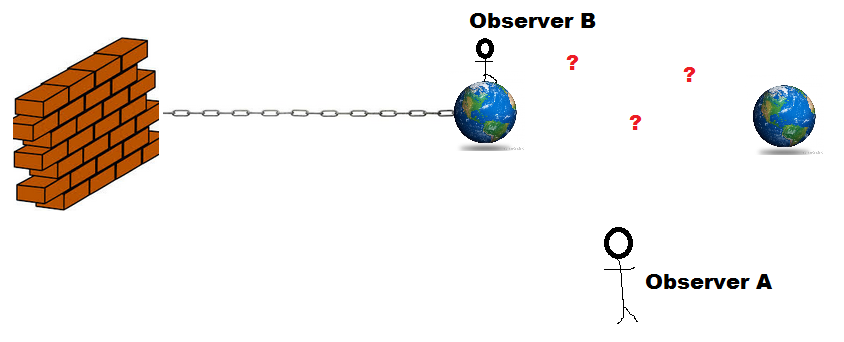
Imagine one planet is chained to a magical wall which could not be moved. OnlyMe, what do you think the outcome of this picture would be? Do you think the fall time of the free planet would be less than, greater than, or equal to the measured fall time if both planets were free? Because the real answer is that this is what Galileo was describing. All objects from feathers to bowling balls to other planets TO BLACK HOLES would all be timed to descend to this chained planet at equal velocities from equal heights.

The fact that the Earth is free floating changes the math.

 

[RJBeery]

Tashja: : http://www.sciforums.com/threads/galileo-was-technically-wrong.142700/

Is the author's argument correct?

Prof. Wasserman:

Technically, it is true that the falling mass attracts the Earth gravitationally, just as the Earth attracts the falling mass. Their relative acceleration is g1+m/M, where m is the mass of the falling mass, M the mass of the Earth, and g is the acceleration of gravity at the surface of Earth, about 9.8 meters per second squared.

Practically, the correction is super-tiny because m is much smaller than M: for a 1 kg mass the effect is about g/6X1024, or about 1.6 X 10^−24 meters per second squared. I believe that is about a factor of 10 billion smaller than the smallest acceleration ever measured in a laboratory but haven't done an exhaustive search.

More precisely, by the way, the relative acceleration also varies with the height h of the falling mass above the surface of Earth i.e. the relative acceleration at height h is approximately g1+m/M−2h/Rwhere R is the radius of Earth. This correction is not so small: for h= 1 meter it is about 3 X 10^−6 meters per second squared. The time to free fall from h=1 meter is about 0.45 seconds without any of these corrections, but of order 60 nanoseconds longer because of the variation of relative acceleration with height. This should be relatively easy to measure.

This was posted in the other thread. For any intellectually honest person this discussion has been irrefutably settled and is over.

 

[Motor Daddy]

Imagine a burning ball of force (read-"the sun") pushing objects known as planets away from it. The more time that elapses the further away the planets get from the sun, which is not to be confused with planets getting closer and crashing into the sun as time elapses. That doesn't happen! Planets don't crash into the sun, they get further away over time!

The second law says I'm right!

 

[el es]

When the mass of a test object is very small compared to the mass of a planet, Newton's Universal Law of Gravitation equation is changed to the gravitational acceleration equation. Notice that m is removed from both sides of the equation.

http://www.physicsclassroom.com/class/circles/Lesson-3/The-Value-of-g

The rings of Saturn are a great example of this. The radius is determined by the objects velocity, not it's mass.

 

[billvon]

Imagine one planet is chained to a magical wall

Now we are chaining planets to brick walls and Motordaddy has started with his crazy. It has become an authentic, homegrown Sciforums thread. All it needs now is Motordaddy to post "I have calculated it to be 4.9473409432423423430128520239953229110393746 seconds so I am right!" and Garbonzo to invoke God. Perhaps we could get Michael to hate Obama and Bells to call someone a misogynist just to round things out.

 

[Motor Daddy]

Now we are chaining planets to brick walls and Motordaddy has started with his crazy. It has become an authentic, homegrown Sciforums thread. All it needs now is Motordaddy to post "I have calculated it to be 4.9473409432423423430128520239953229110393746 seconds so I am right!" and Garbonzo to invoke God. Perhaps we could get Michael to hate Obama and Bells to call someone a misogynist just to round things out.

If I understand you correctly, you're saying you agree with me.

Edit: I don't hide my crazy like Miranda does.

Love that video!

 

[exchemist]

Imagine one planet is chained to a magical wall which could not be moved. OnlyMe, what do you think the outcome of this picture would be? Do you think the fall time of the free planet would be less than, greater than, or equal to the measured fall time if both planets were free? Because the real answer is that this is what Galileo was describing. All objects from feathers to bowling balls to other planets TO BLACK HOLES would all be timed to descend to this chained planet at equal velocities from equal heights.

The fact that the Earth is free floating changes the math.

Stop introducing more metaphors and let's just do the maths, for both frames of reference. Then we'll know.

 

[Neddy Bate]

Yes, Neddy Bate, that's exactly the problem. They apparently believe that the force would only apply to one of the two masses.

Okay, now I understand. They don't deny that the attractive gravitational force is a function of the product of both masses. But they assume the earth to be stationary when calculating the resulting acceleration of the other mass. I see.

 

[exchemist]

Now we are chaining planets to brick walls and Motordaddy has started with his crazy. It has become an authentic, homegrown Sciforums thread. All it needs now is Motordaddy to post "I have calculated it to be 4.9473409432423423430128520239953229110393746 seconds so I am right!" and Garbonzo to invoke God. Perhaps we could get Michael to hate Obama and Bells to call someone a misogynist just to round things out.

The Like button has disappeared again, but….spot-on.

 

[Fednis48]

RJBeery, thanks for bringing my post over to this thread; I didn't mean to contribute to the derailing of a thread on black holes.

tashja's quote of Prof. Wasserman in post #45 is an impeccable qualitative description, so I'm going to try and cover the math. One thing I hope everyone can agree on is the expression for the energy of the system, which is a combination of two kinetic energy terms and the Newtonian gravitational potential formula:

E=kinetic+potential=P^2/2M+p^2/2m+GMm/(X-x)

Here, positions and momenta are along the earth<->object axis, capital {M, X, P} refer to the Earth's mass, position, and momentum, respectively, lowercase {m, x, p} refer to the same properties of the falling object, and G is the universal gravitation constant. Without loss of generality, I have assumed that Earth's position coordinate is higher than the object's; if the reverse is true, the denominator in the potential energy would be (x-X) instead. The equation for a system's energy is its Hamiltonian, so we can use Hamiltonian mechanics (http://en.wikipedia.org/wiki/Hamiltonian_mechanics) to determine the dynamics. We want to compare accelerations, so we're looking for the rate of change of the relative velocity:

d/dt(v_rel)=d/dt(V-v)==d/dt(P/M-p/m)=dP/dt/M-dp/dt/m

Position and momentum are a canonical coordinate pair, so we can say dp/dt=-dH/dx. Note that on the Wikipedia page and in textbooks, position is usually denoted as q instead of x. Plugging this into the above expression:

d/dt(v_rel)=-dH/dX/M+dH/dx/m=-Gm/(X-x)^2-GM/(X-x)^2=-G(m+M)/(x_rel)^2

As RJBeery has been insisting, the result depends on both m and M. If we assume that M>>m, we can drop m from the equation to good approximation; this is the "Galilean approximation".

edit: I anyone else experiencing an issue where anything written in parentheses compiles as TeX?

 

[Trippy]

There is an absurdity in the idea that the "greater mass" is the mass which solely dictates falling times. Galileo's proclamation that falling times are independent of mass were only approximations due to the relative insignificance of the objects he was studying.

How about addressing this:

Only if the blackholes mass was negligible compared to the mass of the earth, for that is the caveat applied to the assertion that you are ignoring.

Instead of tilting at strawmen?

 

[brucep]

Except that while the earth is pulled up toward the bowling ball shortening the distance.., in the case of the golf ball, IT (the golf ball) falls toward the earth faster than the bowling ball does.., also shortening the distance...

This is never an issue, if you always use the earth as the frame of reference for the fall in both cases.., because all of the closing velocity is then attributed to the smaller object. When you try to look at it from the rest frame before the drop you have to take into account that the golf ball falls faster toward the earth than the bowling ball does.., which is exactly balanced by the difference in how fast the earth falls toward the smaller object in each case.

You are wrong! And as been pointed out Newton and Einstein are both right. Take the time to look over, The force of gravity is the same for atoms and baseballs. That should be a larger difference in mass than your bowling and base ball fantasy. And I am sure than even though I don't want to strain myself with the math, the researchers involved had no issue with the math... Without a reference I think I also remember a proposed test with neutrons, but I am unsure and a little skeptical given the short half life of a free neutron.

RJBeery, thanks for bringing my post over to this thread; I didn't mean to contribute to the derailing of a thread on black holes.

tashja's quote of Prof. Wasserman in post #45 is an impeccable qualitative description, so I'm going to try and cover the math. One thing I hope everyone can agree on is the expression for the energy of the system, which is a combination of two kinetic energy terms and the Newtonian gravitational potential formula:

E(kinetic+potential)=P^2/2M+p^2/2m+GMm/(X-x)

Here, positions and momenta are along the earth<->object axis, capital {M, X, P} refer to the Earth's mass, position, and momentum, respectively, lowercase {m, x, p} refer to the same properties of the falling object, and G is the universal gravitation constant. Without loss of generality, I have assumed that Earth's position coordinate is higher than the object's; if the reverse is true, the denominator in the potential energy would be (x-X) instead. The equation for a system's energy is its Hamiltonian, so we can use Hamiltonian mechanics (http://en.wikipedia.org/wiki/Hamiltonian_mechanics) to determine the dynamics. We want to compare accelerations, so we're looking for the rate of change of the relative velocity:

d/dt(v_rel)=d/dt(V-v)==d/dt(P/M-p/m)=dP/dt/M-dp/dt/m

Position and momentum are a canonical coordinate pair, so we can say dp/dt=-dH/dx. (On the Wikipedia page and in textbooks, position is usually denoted as q instead of x.) Plugging this into the above expression:

d/dt(v_rel)=-dH/dX/M+dH/dx/m=-Gm/(X-x)^2-GM/(X-x)^2=-G(m+M)/(x_rel)^2

As RJBeery has been insisting, the result depends on both m and M. If we assume that M>>m, we can drop m from the equation to good approximation; this is the "Galilean approximation".

read the post I wrote to you in the other thread. Tidal accelerations can change the free fall path through spacetime not the rate of free fall. That,

RJBeery, thanks for bringing my post over to this thread; I didn't mean to contribute to the derailing of a thread on black holes.

tashja's quote of Prof. Wasserman in post #45 is an impeccable qualitative description, so I'm going to try and cover the math. One thing I hope everyone can agree on is the expression for the energy of the system, which is a combination of two kinetic energy terms and the Newtonian gravitational potential formula:

E(kinetic+potential)=P^2/2M+p^2/2m+GMm/(X-x)

Here, positions and momenta are along the earth<->object axis, capital {M, X, P} refer to the Earth's mass, position, and momentum, respectively, lowercase {m, x, p} refer to the same properties of the falling object, and G is the universal gravitation constant. Without loss of generality, I have assumed that Earth's position coordinate is higher than the object's; if the reverse is true, the denominator in the potential energy would be (x-X) instead. The equation for a system's energy is its Hamiltonian, so we can use Hamiltonian mechanics (http://en.wikipedia.org/wiki/Hamiltonian_mechanics) to determine the dynamics. We want to compare accelerations, so we're looking for the rate of change of the relative velocity:

d/dt(v_rel)=d/dt(V-v)==d/dt(P/M-p/m)=dP/dt/M-dp/dt/m

Position and momentum are a canonical coordinate pair, so we can say dp/dt=-dH/dx. (On the Wikipedia page and in textbooks, position is usually denoted as q instead of x.) Plugging this into the above expression:

d/dt(v_rel)=-dH/dX/M+dH/dx/m=-Gm/(X-x)^2-GM/(X-x)^2=-G(m+M)/(x_rel)^2

As RJBeery has been insisting, the result depends on both m and M. If we assume that M>>m, we can drop m from the equation to good approximation; this is the "Galilean approximation".

Read my post answering yours in the other thread. Tidal accelerationslerations can change the path of the object through spacetime but it doesn't effect the rate of the falling object. The Newtonian analysis you're trying to do isn't something Newton would be doing. If it was then it would show up in the equation of motion derived from his theory.

 

[paddoboy]

How about addressing this:

Instead of tilting at strawmen?

As well as the odd red herring or two.

 

[RJBeery]

Read my post answering yours in the other thread. Tidal accelerationslerations can change the path of the object through spacetime but it doesn't effect the rate of the falling object. The Newtonian analysis you're trying to do isn't something Newton would be doing. If it was then it would show up in the equation of motion derived from his theory.

Uhh, it DOES show up in the purely Newtonian analysis I did in the opening post of this thread. The equations you're posting about dr/dt are ignoring Newton's third law. And now you're refuting Fednis' math analysis as well as Professor Wasserman's qualitative description!

And you want to be taken as an authority around here?

 

[Trippy]

Uhh, it DOES show up in the purely Newtonian analysis I did in the opening post of this thread. The equations you're posting about dr/dt are ignoring Newton's third law. And now you're refuting Fednis' math analysis as well as Professor Wasserman's qualitative description!

And you want to be taken as an authority around here?

You're sure about that?

From the perspective of a stationary observer taking measurements relative to themself, how can how fast I run towards you change how fast you run towards me? It can't. It's unphysical and nonsenseical.

Two objects, A and B. They have a center of mass.

as long as (m_a) >>> (m_b) then changing the value of (m_b) isn't going to change the rate at which B falls towards the center of mass of the system, it's only going to change the rate at which A falls towards the center of mass of the system.

 

[RJBeery]

You're sure about that?

From the perspective of a stationary observer taking measurements relative to themself, how can how fast I run towards you change how fast you run towards me? It can't. It's unphysical and nonsenseical.

Two objects, A and B. They have a center of mass.

as long as (m_a) > (m_b) then changing the value of (m_b) isn't going to change the rate at which B falls towards the center of mass of the system, it's only going to change the rate at which A falls towards the center of mass of the system.

This is exactly right. Except you're not appreciating that if the Earth falls towards the bowling ball "more quickly" (than, say, towards the golf ball) then the bowling ball has a shorter distance to cover before it impacts the Earth. Not only did I show this in the opening post, Fednis gave a math-based analysis AND we have quotes from actual Physics professors supporting my claim.

The case is closed. Further discussion is futile, but I'm sure that won't stop some folks here.

 

[Motor Daddy]

The case is closed. Further discussion is futile, but I'm sure that won't stop some folks here.

The case is reopened.

If you claim the bowling ball accelerates at the rate of 9.8 m/s^2, then in exactly 1 second the bowling ball traveled 4.9 meters, and has a velocity of 9.8 m/s. Agree?