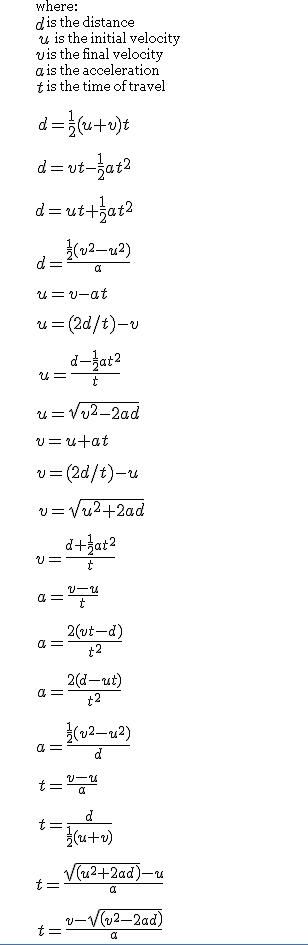Galileo was technically WRONG

RJBeery

RJBeery

Natural Philosopher
Valued Senior Member
Start with variables

r = radius of Earth = 6371000 m
m_e = mass of Earth = 5.972E24 kg
m_gb = mass of golf ball = .05 kg
m_bb = mass of bowling ball = 6 kg
m_bh = mass of black hole at center of Milky Way (est) = 8.2E36 kg
m_o = mass of arbitrary object
F_e.gb = force between Earth and golf ball = .491 N
F_e.bb = force between Earth and bowling ball = 58.92 N
F_e.bh = force between Earth and the black hole = 8.052E37 N
F_e.o = force between Earth and arbitrary object
a_e.gb = acceleration of the Earth towards the golf ball = .00008029 m/s^2
a_gb.e = acceleration of the golf ball towards the Earth = 9.82 m/s^2
a_e.bb = acceleration of the Earth towards the bowling ball = .00963481 m/s^2
a_bb.e = acceleration of the bowling ball towards the Earth = 9.82 m/s^2
a_e.bh = acceleration of the Earth towards the black hole = 1.348E13 m/s^2
a_bh.e = acceleration of the black hole towards the Earth = 9.82 m/s^2 (corrected rounding error)
a_o.e = acceleration of arbitrary object towards the Earth
d = distance between objects = 10 m
d_e = distance Earth falls before collision with object
d_o = distance object falls before collision with Earth
t_e = time Earth falls before collision with object
t_o = time object falls before collision with Earth

F = Gm1*m2/r^2, therefore the Force calculations above were used with the associated variables listed and can be verified here

d = (a*t^2)/2
t = sqrt(2d/a)

For any object 10 m above Earth, we use subscript _o:
t_e = t_o = sqrt(2d_e/a_e.o) = sqrt(2d_o/a_o.e)

This gives us
d_e*a_o.e = d_o*a_e.o
d_o = d_e*a_o.e/a_e.o

We also know that
d = d_e + d_o = 10 m

Substituting we get
d_e + d_e*a_o.e/a_e.o = d
d_e = d / (1+(a_o.e/a_e.o))

This allows us to calculate t
t = sqrt(2d_e/a_e.o) = sqrt(2(d/1+(a_o.e/a_e.o))/a_e.o) = sqrt(2d/(a_o.e+a_e.o))

=========================================
For the golf ball:
t = sqrt(20/(9.82 + .00008029)) = 1.4271101 seconds

For the bowling ball:
t = sqrt(20/(9.82 + .00963481)) = 1.4264164 seconds

For the black hole:
t = sqrt(20/(9.82 + 1.348*10^13)) = .00000121806 seconds
=========================================

The reason most people get this wrong is because it is presumed that the Earth does not also move towards the falling object. It should be obvious that this is the case when the "falling object" is extremely massive (i.e. a black hole) - QED
 
Galileo was technically right if the two masses are dropped at the same time.
 
From another thread:

RJBeery said:
I'm confused, are you saying you don't believe it? If Galileo had dropped his items separately but from the same height he could have measured (with an impossibly accurate timepiece) that they do not in fact hit the ground in the same amount of time.
Click to expand...
Dr_Toad said:
Why should I "believe" a fantasy? In air they hit at different times, but not in a vacuum. Like I said, show me the math, give a concise and cogent description, and prove it.
Click to expand...
RJBeery said:
You need to be careful with your challenges. Do I have your word that you will publicly acknowledge that you're mistaken?
Click to expand...
Dr_Toad said:
If I am, I will apologize.
One caveat: rpenner or Trippy should mediate if I question your maths.
Click to expand...
OnlyMe said:
I am not sure but I believe Dr_Toad's objection would be covered by experimental evidence like, that discussed in his press release from 1999, http://news.stanford.edu/pr/99/atomgravity990825.html.
Click to expand...
paddoboy said:
I'm with Dr Toad on this.
Click to expand...
brucep said:
They proved that 'on tv' during the Apollo project. You'd think they'd seen that during kindergarten class.
Click to expand...
brucep said:
They did the experiment on the moon during the Apollo project. There's probably a YouTube video somewhere in Internet land. RJBerry must have flunked kindergarten for prospective 'natural philosophers'.
Click to expand...
Aqueous Id said:
So if you drop a bowling ball while weighing yourself the scale will read heavier, not lighter. At least until impact, and then you get lighter?
Click to expand...

RPenner, as you can see, Dr_Toad and others are requesting your mathematical acumen in the evaluation of my proof. Thanks in advance! ;)
 
Last edited by a moderator:
RJBeery, are you saying that some folks looked at this equation...

F = G (m_1 * m_2) / r^2

...and concluded that only one of the masses affects the attractive gravitational force between them?
 
rpenner said:
Galileo was technically right if the two masses are dropped at the same time.
Click to expand...
The rate an object falls (free fall) has nothing to do with when It was dropped or the mass of the object in free-fall.
Since Galileo discovered this he's technically right infinite in extent. Unless somebody can show otherwise. Which RJBerry has't done with his juvenile analy
rpenner said:
Galileo was technically right if the two masses are dropped at the same time.
Click to expand...
You think there is some physics which will include force and acceleration in an inertial free fall frame. RJBerry analysis reminds me of a chinglu analysis where he either adds or subtracts, something that should be or shouldn't be included in the physics. Winding up with irrelevant nonsense.
 
Neddy Bate said:
RJBeery, are you saying that some folks looked at this equation...

F = G (m_1 * m_2) / r^2

...and concluded that only one of the masses affects the attractive gravitational force between them?
Click to expand...
Yes, Neddy Bate, that's exactly the problem. They apparently believe that the force would only apply to one of the two masses.
 
Last edited by a moderator:
brucep said:
The rate an object falls (free fall) has nothing to do with when It was dropped or the mass of the object in free-fall.
Since Galileo discovered this he's technically right infinite in extent. Unless somebody can show otherwise. Which RJBerry has't done with his juvenile analy

You think there is some physics which will include force and acceleration in an inertial free fall frame. RJBerry analysis reminds me of a chinglu analysis where he either adds or subtracts, something that should be or shouldn't be included in the physics. Winding up with irrelevant nonsense.
Click to expand...
If two objects are in free fall and one object falls a shorter distance before hitting the ground, I have to assume that you would agree it would do so in less time, correct? That's the crux here. The Earth is pulled up toward the bowling ball (or the moon, or the black hole) with a greater force than with the golf ball, therefore the bowling ball (et al) hit the Earth in less time because they are falling a shorter distance.
 
RJBeery said:
If two objects are in free fall and one object falls a shorter distance before hitting the ground, I have to assume that you would agree it would do so in less time, correct? That's the crux here. The Earth is pulled up toward the bowling ball (or the moon, or the black hole) with a greater force than with the golf ball, therefore the bowling ball (et al) hit the Earth in less time because they are falling a shorter distance.
Click to expand...

Except that while the earth is pulled up toward the bowling ball shortening the distance.., in the case of the golf ball, IT (the golf ball) falls toward the earth faster than the bowling ball does.., also shortening the distance...

This is never an issue, if you always use the earth as the frame of reference for the fall in both cases.., because all of the closing velocity is then attributed to the smaller object. When you try to look at it from the rest frame before the drop you have to take into account that the golf ball falls faster toward the earth than the bowling ball does.., which is exactly balanced by the difference in how fast the earth falls toward the smaller object in each case.

You are wrong! And as been pointed out Newton and Einstein are both right. Take the time to look over, The force of gravity is the same for atoms and baseballs. That should be a larger difference in mass than your bowling and base ball fantasy. And I am sure than even though I don't want to strain myself with the math, the researchers involved had no issue with the math... Without a reference I think I also remember a proposed test with neutrons, but I am unsure and a little skeptical given the short half life of a free neutron.
 
RJBeery said:
Yes, Neddy Bate, that's exactly the problem. They apparently believe that the force would only apply to one of the two masses. (For some reason, they also continue to post to an unrelated thread on this subject)
Click to expand...

So are you saying the Earth accelerates toward the bowling ball, even as the bowling ball accelerates toward the Earth, and, if so, what happened to that 9.8 m/s² g-field? Because as the Earth rushes toward the bowling ball, g, which is a function of r, now needs to be treated as g(r(t)). I don't see where you covered that in your mathematical analysis.

What now?
 
Aqueous Id said:
So are you saying the Earth accelerates toward the bowling ball, even as the bowling ball accelerates toward the Earth, and, if so, what happened to that 9.8 m/s² g-field? Because as the Earth rushes toward the bowling ball, g, which is a function of r, now needs to be treated as g(r(t)). I don't see where you covered that in your mathematical analysis.

What now?
Click to expand...
The 9.82 m/s^2 is unchanged in my analysis. The numbers I use in my analysis in the OP are DERIVED via F=Gm1*m2/r^2. They are NOT simply given by convention! The difference in g(r(t)) is indeed ignored, but that is inconsequential because the field gradation between 10 meters and the ground of the Earth would be the same for all objects, so it is considered to be a constant at the value derived at 10 meters. The result (or more specifically, the conclusion) would be the same either way. I'm holding out hope that you, Aqueous Id, are clever enough to grasp this proof because it appears the others who are (i.e. rpenner) don't have the intellectual fortitude to publicly admit it.
 
Last edited:
RJBeery said:
The 9.82 m/s^2 is unchanged. The numbers I use in my analysis in the OP are DERIVED via F=Gm1*m2/r^2. They are NOT simply given by convention! The difference in g(r(t)) is indeed ignored, but that is inconsequential because the field gradation between 10 meters and the ground of the Earth would be the same for all objects, so it is considered to be a constant at the value derived at 10 meters. The result would be the same either way. I'm holding out hope that you, Aqueous Id, are clever enough to grasp this proof because it appears the others who are (i.e. rpenner) don't have the intellectual fortitude to publicly admit it.
Click to expand...

Let me get this straight. You are saying that if I drop a bowling ball from a height of 4.91 meters above the surface of the earth, that it will take 1 second for the ball to impact the surface of the earth?
 
I reckon 4.91 meters would take 1 second, roughly; unless the mass was vastly larger than a golf ball. (presuming your post is correct! I did not verify)
 
The heavier item may have a greater attraction but it also has great resistance to change...Intertia:
The lighter item has less attraction, and also less Inertia and less resistance to change/movement/falling.

So we have one item with great gravitational attraction and more intertia, fighting that attraction...and the other have less gravitational attraction but also less Inertia fighting the gravitational pull.
Guess what? The two effects balance each other out, so that they hit the ground at the same time.

Galileo was right!
 
RJBeery said:
I've given you the tools to do the calculation yourself big guy.

t = sqrt(2d/(a_o.e+a_e.o))
Click to expand...

I've given YOU the tools.

test_zpscbfb9650.jpg
 
You must log in or register to reply here.
Back
Top