exchemist
Valued Senior Member
Yes. It is crystal clear. To me, at least.
But I have not the patience for another of your interminable disputes about physics. Try someone else.
Last edited:
do the particles ever collide in QED
- Thread starter Arlich Vomalites
- Start date
Yes. It is crystal clear. To me, at least.
But I have not the patience for another of your interminable disputes about physics. Try someone else.
No problem.
The first summation expresses the electric field in a particular basis. The second sum is the magnetic field. The circle with the cross in it is an operator for the outer product between the two sums. On the right-hand side we have the tensor components in terms of the tensor product formed by the outer product.
Sure I can. When a charged particle is placed in a field (caused by one or more other charged particles), that charge experiences a force in the direction of the net field if the charge is positive, and a force in the opposite direction if the charge is negative.
But I thought I'd already explained this to you mathematically in my previous post. Didn't you understand?
I think that because you don't know what a tensor is, you don't understand why it doesn't "point" like a vector does. When you talk about "arrowheads", I assume you're talking about the ones on the field diagram. Those are like electric field vectors, and they do point. There is an inward or outward field depending on which direction those arrows point. You even provided the diagrams yourself. As for "chirality", I doubt you know what that term refers to.
I already walked you through this. An electron has only an electric field when it is stationary. If it moves, it has an electric and a magnetic field. Call that the electromagnetic field if you want to.
Yes it does. That's relativity.
No. If you remain stationary, there's no magnetic field from your electron. Only moving charges create magnetic fields. Also, I don't get what you mean by I feel the electron "swirling". What does that mean? Magnetic forces aren't "swirly" forces. They point in straight lines, just like other forces. Forces are vectors quantities.
Define "chirality" for me, please.
Your assertion that the field of a single charge points "both ways" is just wrong. I don't know where you get this stuff.
An electromagnetic field is just electric and magnetic fields, nothing more. Of course, you can have the electric part pointing one way and the magnetic part pointing another way. Suppose they are at right angles, as they are in an electromagnetic wave. Tell me, then, Farsight. Which way does the "electromagnetic" field then point, and how do you work it out? Please show me the maths, too.
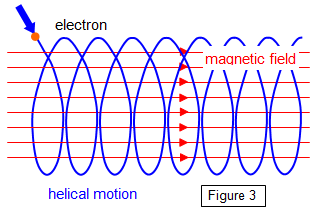
That's a pretty picture, but it doesn't tell us anything about electromagnetic fields.Strictly speaking, it doesn't really point in any direction. But since North is a whole host of directions and we can understand North, we can also understand the "direction" of the electromagnetic field. It's the same as the direction that this thing is spinning:
I was mistaken: I just saw it on another one of his pages. It's very similar to some other pictures.
LOL! We know all that. It doesn't tell us anything. Quarkhead knows this, that's why he's done a runner again.
But why Daddy? Why?
What previous post? I'm looking back pages, you haven't explained anything. $$\vec{F}=q\vec{E}$$ is just a restatement of your assertion that the direction of the force depends on whether the charge is negative or positive. You haven't explained why.
I challenged Quarkhead to explain why he can't tell the electrons from the positrons. Which ought to make it clear that there is no inward or outward field. But he's scarpered. I do know what chirality means.
No, it has an electromagnetic field! This is basic stuff James.
No. Your motion alters the way you see it. It doesn't change just because you moved.
Aaaaagh! They don't create magnetic fields! The field is the electromagnetic field. read this.
An electron moves in a helical path in a magnetic field. A charged particle goes around the "magnetic field lines". LIke this:
Imagine you're holding the electron and you're moving through the solenoid.
No. Go and look it up.
I didn't say that. I took the arrowheads off my depiction, and I said the electromagnetic field points all ways.
The electromagnetic field points this way:
I started a thread showing how you work it out. Somebody moved it to alternative theories. The maths is the maths you're used to, you just have to appreciate that E and B aren't fields, they're forces that result from the interaction of two electromagnetic fields. Or more of course. But to understand it you start with two charged particles.
It ought to.
Arlich Vomalites
Registered Member
Thanks again tashja, thanks Prof. Lincoln
Yes, it seems certain that electrons don't physically collide in the Standard Model QED. That is because they have zero size as Prof. Lincoln said.
Nevertheless I am interested in the finite size electron models, which can lead into that the electrons collide
physically, analogous to a "direct impact" as Prof. Wilczek said. I think that these kind of electrons don't need to be composite objects like protons are, although these kind of finite size electrons can fuse into each others during the Big Bang.
Why this is so, is that because I think that a half of an electron is just a half of an electron. I know this may sound stupid or obvious. But if you compare the case with protons: half of a proton if not anymore half of a proton, because the proton is a composite object whose parts are something else.
If two finite size electrons can fuse into each others, the product will simply be an object consisting of
two electrons.
According to a Standard Model Big Bang, when three quarks fuse into each others, the product will be
the proton, not merely an object consisting of three quarks. In this sense, the proton is more than its
constituents, the three quarks. But two electrons are just two electrons always, even if they are capable
of taking part in a fusion reaction during the Big Bang.
What Don Lincoln told tashja was a simplified popscience version for kids. Have a read of Matt Strassler's article on virtual particles:
"The best way to approach this concept, I believe, is to forget you ever saw the word “particle” in the term. A virtual particle is not a particle at all... "
Well, you can do an argument from authority, Farsight, but can you do a single physics example with some mathematics? Just show us the mathematics for an electron interaction with your vortices.
It's just the same old $$|\mathbf F|= 1 / (4\pi\varepsilon_0) {|q_1q_2|\over r^2}\qquad$$ which results from vorticial attraction and repulsion. Counter-rotating vortices attract, co-rotating vortices repel. The electron and the positron aren't throwing photons back and forth, they're spinors. Vortices. Only they aren't my vortices, they're Maxwell's.
That is a lie.
Show us the dynamics of the particles in the vortices and how they produce the equation above that you are trying to steal to bolster your religious claims.
Arlich Vomalites
Registered Member
Do you mean that the charge of the electron arises are a consequence of its rotation ?
Leading to the conclusion that if the electron did not rotate, it would not possess its charge?
these continuous shenanigans are pathetic.
*Sigh* How many more times - fields do NOT "point", not even vector fields..Maxwell's equations (as re-written by Heavyside) contain 2 differential operators on the EM (vector) field, known as the curl and the divergence (div)
Since these operators have directional derivatives as components, one can think of these operators as causing the field to "point". And accordingly one is free to change signs at will. So that the curl of a vector field - itself a vector field - can be taken as counter-clockwise or clockwise, and the divergence of a vector field - a scalar field - can be taken as being directed toward the source or away from it.
I stress, these are the result of applying differential operators to the field, not, repeat NOT the field itself
Yes. In gamma-gamma pair production we start with two 511keV photons moving linearly at c. Each is an electromagnetic field variation. Imagine that you displace them sideways to "wind" them into a tight circular path, such that for one of them the -ve field variation is on the outside, and for the other the +ve field variation is on the outside. They're still waves, you can still diffract them, but now they're going round and round at c rather than linearly at c. They look like standing waves, see atomic orbitals where "the electrons do not orbit the nucleus in the sense of a planet orbiting the sun, but instead exist as standing waves". Standing wave, standing field. Then if you let them interact with each other they "unwind" each other, and you've got two 511keV photons again. Check out the Einstein-de Haas effect which "demonstrates that spin angular momentum is indeed of the same nature as the angular momentum of rotating bodies as conceived in classical mechanics".
Yes. A cyclone has intrinsic spin. It's intrinsic because it makes it what it is. If you take the rotation away from a cyclone, it's just wind. An electron has intrinsic spin too. If you take the rotation away from an electron, it's just light. What's the difference between the wind and a cyclone? The rotation. What's the difference between a 511keV photon and an electron? The rotation. What's the difference between a cyclone and an anticyclone? The rotation. What's the difference between an electron and a positron? The rotation. Don't ask me why this isn't common knowledge. It ought to be. The Einstein-de Haas effect was discovered a hundred years ago. If you ask around saying what actually happens in pair production nobody will tell you about displacement current. All you get is flannel. Like the photons pop out of existence and the electrons pop into existence. IMHO it's absurd.
Last edited:
The reason it isn't common knowledge is that it is entirely your fantasy. You have no equations that relate the spinning of an electron, in your sense, to the observed spin behavior of an electron or to the charge of an electron.
Yet as the author of the wikipedia page you love so much writes, the Einstein-de Haas effect does not indicate that electron spin is the same as mechanical rotation, as you claim. To quote, "As for your other question, electron spin is an angular momentum, however one whose origin is quantum-mechanical (as I indicate in the main text): it is described by an operator whose various components do not commute. The nature of your question (your emphasis on "mechanical") suggests that perhaps you should consult some elementary book on quantum mechanics. In such case, the book by David J. Griffiths (Introduction to Quantum Mechanics) would be a very appropriate choice (Chapter 4, Section 3, gives a brief account of angular momentum in quantum mechanics and Chapter 4, Section 4, introduces spin; in this section it is nicely shown how spin is algebraically related to angular momentum in quantum mechanics: the components of the corresponding operator satisfy the same Lie algebra as the components of the operator that one obtains on quantising the classical angular momentum in accordance with the correspondence principle). My remark that the origin of electron spin is quantum mechanical refers to the fact that the quantum-mechanical operator for electron spin cannot be directly deduced by quantising a classical counterpart (such counterpart does not exist); it can only be introduced through using the Lie algebra satisfied by the components of the quantum-mechanical angular momentum operator as the starting point."
Farsight, I keep asking for a reference to any experiment that collides two photons directly. So far you have failed to do so.
Yes, there are some proposals for equipement design that might, and I emphasize might, make it possible sometime in the future, but even your past references have said photon-photon or gamma-gamma collisions have not been observed.
Yes, curl and divergence, like what you can see here on the right:
Of course clockwise and counterclockwise isn't enough for 3D curl, but I know what you mean:
Note though that the "source and sink" aspect of electromagnetic teaching is IMHO badly misleading. Hence no arrowheads above. Hence you couldn't answer my question about the electrons and positrons.
When you try to depict the electromagnetic field, you don't have a lot to play with.
It's the Breit-Wheeler process. See this:
"However, in 1997, researchers at the Stanford Linear Accelerator Centre were able to conduct the so-called multi-photon Breit–Wheeler process using electrons to first create high-energy photons, which then underwent multiple collisions to produce electrons and positrons, all within same chamber."
Don't doubt it. It's just electron-positron annihilation in reverse.
They have been observed. See above. What hasn't been done is a "pure" process where you start with photons.
Which is the first time to my knowledge you have used these terms in this thread
As for your "proof" using (once again) your silly graphics, please explain what they mean. What is the differential operator on the RHS of the equality? Why are you "adding" differential operators?
I can tell you this, though. From elementary operator theory, the divergence of the curl is zero. Want to see the proof? Or better, provide a (non-graphical) one of your own?
I await your reply with high expectations........
That's part of the problem I specified direct photon-photon collision. Your reference is implied/inferred or interpreted as resulting in photon-photon collisions. From your link which describes the theoretical process,
"... as of 2014, it has never been observed in practice because of the difficulty in preparing colliding gamma ray beams. ..."
What you keep implying is that gamma-gamma pair production has been directly observed. You even provide little diagrams that show it that way. Yet your own references, including the one above, all include the disclaimer that no direct observation of photon-photon collision has.., ever.., been observed.
You use the reference dishonestly. Just like quoting out of context.