We've had the 3D plot:
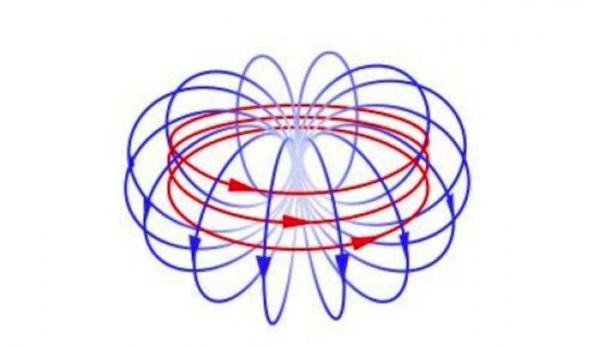
OnlyMe put it up. It's like the Williamson / van der Mark electron:

Which is like the ring torus:

Which you inflate to the spindle-sphere bispinor:

See Adrian Rossiter's Antiprism torus animations. Think of this animation as something like "the eye of the storm", surrounded by frame-dragged space. Co-rotating vortices repel, counter-rotating vortices attract.

Two of these things with the same chirality will move apart. With the opposite chirality they'll move together. The positron has the opposite chirality to the electron.
PS: Weren't you going to explain some maths?

OnlyMe put it up. It's like the Williamson / van der Mark electron:

Which is like the ring torus:

Which you inflate to the spindle-sphere bispinor:

See Adrian Rossiter's Antiprism torus animations. Think of this animation as something like "the eye of the storm", surrounded by frame-dragged space. Co-rotating vortices repel, counter-rotating vortices attract.
Two of these things with the same chirality will move apart. With the opposite chirality they'll move together. The positron has the opposite chirality to the electron.
PS: Weren't you going to explain some maths?

