Just a thought if we can see right back to the start of universe which has been expanding, how come the light has taken that long to get here, surely at the time the light left we would have been closer to every point in the universe than the time the light from the beginning of the universe has taken to reach us.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Center of Universe?
- Thread starter eram
- Start date
- Status
- Not open for further replies.
@origin: yeah I skipped to the crucial part using youtube url codes. It has to do with an exploding billiard ball.
If that billiard ball was the only thing that existed in the entire universe, we would be able to deduce the position of the universe's center of mass.
If Homer Simpson's floating donut was the only thing that existed in the entire universe, the center of mass is in the hole, not the dough. And it would also be the center of mass of the entire universe.
So if there is a finitie amount of mass in this universe, the universe has a center of mass. If there are infinite quantities of mass, but we know how this mass is distributed, we can still find the center of mass.
Also, I was wrong about the imaginary straight line. We cannot measure absolute velocities or positions. However, we can measure absolute distance of an object from the center of mass.
If that billiard ball was the only thing that existed in the entire universe, we would be able to deduce the position of the universe's center of mass.
If Homer Simpson's floating donut was the only thing that existed in the entire universe, the center of mass is in the hole, not the dough. And it would also be the center of mass of the entire universe.
So if there is a finitie amount of mass in this universe, the universe has a center of mass. If there are infinite quantities of mass, but we know how this mass is distributed, we can still find the center of mass.
Also, I was wrong about the imaginary straight line. We cannot measure absolute velocities or positions. However, we can measure absolute distance of an object from the center of mass.
It is the same problem as trying to determine absolute motion. There may be some rock somewhere that God can look at from outside the universe and he can say, "Yep, that rock is not moving and everything else in the universe is moving relative to that stationary rock". But you can't ever under any circumstace determine that. The center of the universe is essentially the same situation - God probably knows but he's not telling and you cannot ever detect it.
The only caveat to this is, when my daughter was about 13 she was pretty sure she was the center of the universe.
how old is your daughter now? Lol.
But if the universe had a finite amount of mass, we could measure the mass and relative position of each object in the universe, and calculate the center of mass.
Just a thought if we can see right back to the start of universe which has been expanding, how come the light has taken that long to get here, surely at the time the light left we would have been closer to every point in the universe than the time the light from the beginning of the universe has taken to reach us.
We would have been closer to every point than the time? I don't think you can equate distance with time Gorlitz.
I don't think you can equate distance with time Gorlitz.
Are you sure about that?
@origin: yeah I skipped to the crucial part using youtube url codes. It has to do with an exploding billiard ball.
If that billiard ball was the only thing that existed in the entire universe, we would be able to deduce the position of the universe's center of mass.
If Homer Simpson's floating donut was the only thing that existed in the entire universe, the center of mass is in the hole, not the dough. And it would also be the center of mass of the entire universe.
So if there is a finitie amount of mass in this universe, the universe has a center of mass. If there are infinite quantities of mass, but we know how this mass is distributed, we can still find the center of mass.
Also, I was wrong about the imaginary straight line. We cannot measure absolute velocities or positions. However, we can measure absolute distance of an object from the center of mass.
Maybe these will help.
Center of the universer.
Big band and expansion of the universe.
icarus2
Registered Senior Member
Center of the universe
Space doesn't expand. New proof of Hubble's law and Center of the universe
http://vixra.org/abs/1203.0044
This is personal hypothesis(nonmainstream). Therefore, carefully read it.
In my opinion - [ We can define the center of the universe and find it. ]
========
Hubble's law isn't a matter only explained by special condition such as "center of the universe" or a new concept that we haven't experienced such as "expansion of space".
Hubble's law is valid is a very wide area in 3 dimensional space when the initial speed of galaxies is much larger than the velocity change by deceleration and acceleration (in the same meaning, when velocity change by deceleration and acceleration is smaller compared to initial speed).
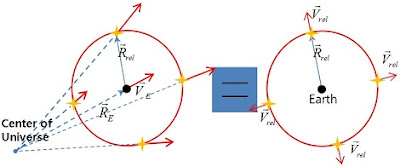
Two situations are same.
========
--- Icarus2
Mechanical Universe 15 - Conservation of Momentum - YouTube
Provided no external forces act on a system, the system's center of mass is always in an inertial frame.
If we consider the entire universe as a system, and assume that no external forces can act on the universe, then the universe has a center of mass. In other words, a center!
Space doesn't expand. New proof of Hubble's law and Center of the universe
http://vixra.org/abs/1203.0044
This is personal hypothesis(nonmainstream). Therefore, carefully read it.
In my opinion - [ We can define the center of the universe and find it. ]
========
Hubble's law isn't a matter only explained by special condition such as "center of the universe" or a new concept that we haven't experienced such as "expansion of space".
Hubble's law is valid is a very wide area in 3 dimensional space when the initial speed of galaxies is much larger than the velocity change by deceleration and acceleration (in the same meaning, when velocity change by deceleration and acceleration is smaller compared to initial speed).

Two situations are same.
========
--- Icarus2
Why do objects that are farther from the center of the universe move faster away from the center?
You idea I believe is that the galaxies are moving through space, not that space is expanding. If that is true then galaxies that we observer that are farthest from the center of the universe are moving faster than the speed of light, which is a violation of SRT. How do you explain that?
You idea I believe is that the galaxies are moving through space, not that space is expanding. If that is true then galaxies that we observer that are farthest from the center of the universe are moving faster than the speed of light, which is a violation of SRT. How do you explain that?
icarus2
Registered Senior Member
I am sorry. I apologize for my poor English. Refer to my paper!Why do objects that are farther from the center of the universe move faster away from the center?
In my opinion,
After an accelerating expansion (such as inflation) of early universe has almost finished, particles started to have some velocity.
This velocity distribution naturally has higher velocity when it is further away from the center of the universe and has lower velocity when it is closer to the center.
A. Big bang simulation in the zero energy universe
[Video for Big bang Simulation]
http://www.youtube.com/watch?v=SRUqQM2FfNU

Fig.1.Velocity distribution of galaxies at early universe.
Red arrows show the velocity vector of particles. It can be known that the magnitude of velocity vector is bigger as it become further from the center.
Even if the velocity of particles is zero in the early universe, there are particles with higher velocity in further areas from the center and particles close to the center have relatively low velocity by inflation (an accelerating expansion). When positive mass gravitationally contracts to form a galaxy, momentum must be conserved, so higher initial velocity continues to exist as it becomes further away from the center of universe.
B. Natural distribution of velocity in the 3D space
Thinking in another way, 3 dimensional space can be divided into 3 areas (from the center) to far, middle, and close area. Even if the velocity of the far area is lower than the middle area, middle area particles exceed far area particles when time passes because the velocity of middle particles are higher. As a result, velocity distribution of particles shows that the velocity of far areas is highest, middle area is second, and the close area becomes third.
C. Velocity distribution when some kind of anti-gravitational source exists
If some kind of anti-gravitational source in 3 dimension exists, M exists with even density, the above velocity distribution can exist.
$$m\vec a = + \frac{{G(\frac{{4\pi }}{3}r^3 \rho )m}}{{r^2 }}\hat r$$
$$\vec a = + \frac{{4\pi G}}{3}\rho r\hat r$$
If anti-gravitational source is evenly distributed in accelerating expansion time like the inflation of early universe, a bigger acceleration a exists as r becomes larger and velocity distribution has a higher velocity as the radius of the universe becomes larger. As a result, higher velocity exists for particles of far area from the center of the universe after inflation ends.
The 3 explanations shown above mean that higher velocity for larger R(distance from the center of universe) after inflation in the early universe isn't a peculiar phenomenon. If speed in small area in the early universe distributes from 0 to c and if some time passes, velocity distribution will be in order as above.
Yes!You idea I believe is that the galaxies are moving through space, not that space is expanding.
Inflation - expansion faster than lightIf that is true then galaxies that we observer that are farthest from the center of the universe are moving faster than the speed of light, which is a violation of SRT. How do you explain that?
To explain the flatness and horizon problem, expansion faster than light (inflation) was assumed. However, positive energy and negative energy are cancelled in the zero energy universe. So zero energy universe is flat. Therefore to explain flatness, there is no need to assume expansion faster than light.
The horizon problem occurs from the wrong Hubble radius which is derived from the assumption that space expands. If particles don't have velocity faster than light, all areas in the early universe will be inside the area of light(radiation) and are all causally connected. Therefore, thermal equilibrium takes place.
In my opinion,
Horizon problem doesn't occur and expansion faster than light isn't needed.
Inflation - expansion faster than light
To explain the flatness and horizon problem, expansion faster than light (inflation) was assumed. However, positive energy and negative energy are cancelled in the zero energy universe. So zero energy universe is flat. Therefore to explain flatness, there is no need to assume expansion faster than light.
An expansion of space that is faster than c does not violate SRT, however something moving in space faster than c does violate SRT.
Due to the expansion of space distant objects are receding from us faster than c.
So the question remains, how does your idea address this problem?
Fraggle Rocker
Staff member
All men think that way.Based on this analysis we are at the center of the universe!
icarus2
Registered Senior Member
We observed the redshift and then, we estimate the scale factor, velocity~
I apologize for my poor English.
======
Due to the expansion of space distant objects are receding from us faster than c.
======
Yes!, “Due to model of the expansion of space”
We don’t know(or observe) velocity of distant galaxy. We observed the redshift and then, we estimate the scale factor, velocity, distance….
Key point of problem, $$R = \frac{1}{{1 + z}}$$, it is derived from assumption that space is expanding. (R is scale factor)
If space does not expanding, R=1/(1+z) is wrong. Therefore velocity and distance are also wrong.
If my model is right, red shift comes from the Doppler shift of light and implies that the existing equation of red shift should be revised.
Doppler shift : $$ z = \sqrt {\frac{{1 + \frac{V}{c}}}{{1 - \frac{V}{c}}}} - 1$$
When space doesn't expand, the maximum value of recession velocity will become light velocity c.
The two models($$R = \frac{1}{{1 + z}}$$ , $$ z = \sqrt {\frac{{1 + \frac{V}{c}}}{{1 - \frac{V}{c}}}} - 1$$ ) show similar results in close galaxies(z<2), but show difference in far galaxies.
(Ref : Bradley W. Carroll, Dale A. Ostlie. Introduction to Modern Astrophysics. 2nd Edition. Pearson Education, Inc.)
In the standard model, if z>1.46, recession velocity exceeds the speed of light.
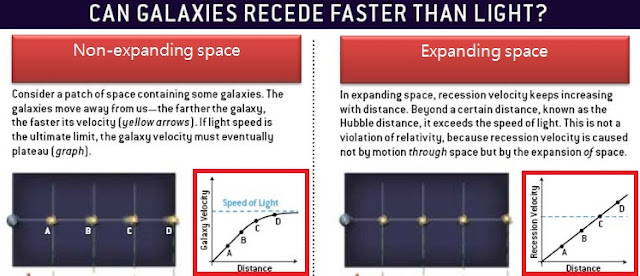
I am sorry.An expansion of space that is faster than c does not violate SRT, however something moving in space faster than c does violate SRT.
Due to the expansion of space distant objects are receding from us faster than c.
So the question remains, how does your idea address this problem?
I apologize for my poor English.
======
Due to the expansion of space distant objects are receding from us faster than c.
======
Yes!, “Due to model of the expansion of space”
We don’t know(or observe) velocity of distant galaxy. We observed the redshift and then, we estimate the scale factor, velocity, distance….
Key point of problem, $$R = \frac{1}{{1 + z}}$$, it is derived from assumption that space is expanding. (R is scale factor)
If space does not expanding, R=1/(1+z) is wrong. Therefore velocity and distance are also wrong.
If my model is right, red shift comes from the Doppler shift of light and implies that the existing equation of red shift should be revised.
Doppler shift : $$ z = \sqrt {\frac{{1 + \frac{V}{c}}}{{1 - \frac{V}{c}}}} - 1$$
When space doesn't expand, the maximum value of recession velocity will become light velocity c.
The two models($$R = \frac{1}{{1 + z}}$$ , $$ z = \sqrt {\frac{{1 + \frac{V}{c}}}{{1 - \frac{V}{c}}}} - 1$$ ) show similar results in close galaxies(z<2), but show difference in far galaxies.
(Ref : Bradley W. Carroll, Dale A. Ostlie. Introduction to Modern Astrophysics. 2nd Edition. Pearson Education, Inc.)
In the standard model, if z>1.46, recession velocity exceeds the speed of light.

Last edited:
I'm not sure how we could possibly know that distant objects are receding from us faster than c. From what I've read c-violation (via space expansion) is required to get Big Bang models to jibe but...today? Or is the theory simply that if we accept space expansion at all then c-violation is theoretically possible?An expansion of space that is faster than c does not violate SRT, however something moving in space faster than c does violate SRT.
Due to the expansion of space distant objects are receding from us faster than c.
So the question remains, how does your idea address this problem?
I'm not sure how we could possibly know that distant objects are receding from us faster than c. From what I've read c-violation (via space expansion) is required to get Big Bang models to jibe but...today? Or is the theory simply that if we accept space expansion at all then c-violation is theoretically possible?
Look at this.
The galaxies that we can observe that are "12 billion light years away" certainly have a recession velocity > c. We are seeing the galaxies as they were 12 billion years ago, which means when the light was emitted they were much closer than 12 billion light years away and they are much further away than 12 billion ly now. As the distance has increased the light that is emitted from them now will never reach earth because they are receding [now] at greater than c.
An expansion of space that is faster than c does not violate SRT, however something moving in space faster than c does violate SRT.
Due to the expansion of space distant objects are receding from us faster than c.
People keep saying glib things like that, but they never provide the scientific physical explanation/mechanism that justifies claiming space expansion causes universal recession motion component of distant galaxies.
Proper motion through space is all that can be observed directly, even in the matter-affected gravity-well conditions of space regions in close proximity to our local energy-matter.
So the question is and always has been: How does 'expanding space' actually couple physically to galactic energy-matter in order to cause and add the alleged recession motion (moving with space) component to a galaxy's own proper motion (moving through space)?
Until the actual physical space-to-galaxy coupling mechanism which is claimed to effect a universal recession (with space) velocity component in addition to a galaxy's normal directly observable proper (through space) velocity component, then it is all conjecture as to what creates the inferred 'expanding space' illusion which is glibly trotted out without any scientific physical explanation/mechanism as to what couples space to a galaxy in order to add that hypothesized but not explained 'big bang' recession velocity component to that galaxy.
If one merely invokes 'dark energy' etc etc etc, then again it behooves one to scientifically explain the physical coupling mechanism which can effect the alleged additional with space recession velocity component above and beyond a galaxy's normal proper through space motion.
I now ask you directly and ever so politely, origin: Have you or anyone else ever provided the physical explanation/mechanism that couples space to matter/energy such that said space's alleged 'expansion' can carry galaxies along with it as claimed by you and others?
Back briefly again later today if I can (else tomorrow) to check for your scientific no-nonsense response to that scientific no-nonsense question. Thanks in advance.
Later!
I now ask you directly and ever so politely, origin: Have you or anyone else ever provided the physical explanation/mechanism that couples space to matter/energy such that said space's alleged 'expansion' can carry galaxies along with it as claimed by you and others?
Let's step back and look at this for just a moment:
1. There is a series of observations about the universe.
2. A theory was put forward to explain the observations (the BB and the expansion of space).
3. Predications were made based on the theory.
4. Data was later obtained that validated the predictions.
5. New data continues to support the BB.
Does the BB answer all questions about the universe - no.
How can the expansion of the universe make the galaxies move with the expansion? My questions is how could the galaxies not move with the expansion of the universe? The answer is local gravity could prevent it - which is what we see.
I ever so politely ask you to try and use your noggin, instead of just enthusiastically embracing every hair brained idea that is labeled as non-mainstream.
Let's step back and look at this for just a moment:
1. There is a series of observations about the universe.
2. A theory was put forward to explain the observations (the BB and the expansion of space).
3. Predications were made based on the theory.
4. Data was later obtained that validated the predictions.
5. New data continues to support the BB.
Does the BB answer all questions about the universe - no.
How can the expansion of the universe make the galaxies move with the expansion? My questions is how could the galaxies not move with the expansion of the universe? The answer is local gravity could prevent it - which is what we see.
I ever so politely ask you to try and use your noggin, instead of just enthusiastically embracing every hair brained idea that is labeled as non-mainstream.
I don't embrace every hairbrained idea. Openmindedness 'entertains' ideas without necessarily 'accepting' them.
But in any case, the OP/other idea/s is not what I asked you about. I asked you about what you claimed in that answer to icarus2. No more. No less. So please disabuse yourself of whatever impression you have made for yourself that I am asking/accepting about anything else. OK?
Now, as to your reply as to the science:
You ask yourself
origin said:...how could the galaxies not move with the expansion of the universe? The answer is local gravity could prevent it - which is what we see."
Your question there 'presupposes' without scientific justification that a) the space 'does' expand and b) galaxies 'must' move with that space. And the rest there I already pointed out was the case in gravity-wells locally, so you have 'answered' nothing new there either. Which only leads back to my original question. So, for the second time...
You claim that space 'expands'; what then is supposed to physically (not metaphysically) couple that 'expanding space' to galaxies to effect their universal recession motion (with expanding space) component above and beyond galaxies proper (through space) motion?
You effectively evaded the question by simply presupposing the very things which were the central aspects under question to you.
Please try again without the circuitous reasoning and presuppositions; and try to keep to answering my question rather than introducing your own personal impressions about what I do or do not accept when I fairly entertain ideas regardless of provenance.
My original question to you was direct, clear, scientific and polite.
Please make your answer likewise regarding whether you can or cannot provide the supporting explanation/mechanism for 'coupling galactic recession' motion to the 'expanding space' as hypothesized according to your initial reply to icarus2.
Thanks.
I now ask you directly and ever so politely, origin: Have you or anyone else ever provided the physical explanation/mechanism that couples space to matter/energy such that said space's alleged 'expansion' can carry galaxies along with it as claimed by you and others?
You really have to be kidding!
When you talk about space or spacetime and matter, you have to be referring to general relativity. General relativity is a extremely successful theory, describing the geometry and dynamics of objects in space/spacetime. Yes there are beginning to be some observations that do not quite fit, requiring the additions of dark mater and dark energy. That takes nothing away from the success of GR and it's improvement compared to Newtonian Dynamics which it replaced or superseded.
Generql Relativity has never even attempted to explain the mechanism of those interactions. It says space and matter interact dynamically and describes that interaction successfully. It says nothing about the mechanism(s) or why of those interactions.
I keep bring this up, but again there have been and are continuing attempts to come up with explanations of the mechanisms from the perspective of QM. There has been no entirely sucessful model/theory, that I am aware of.., yet.
Understanding that you are asking a question that you should know has no answer, makes the whole dialog seem to be at about the same level as a five year old who has just learned the word why.
Do your really think there is a scientific answer to your question?...., that remains consistent with the science folder this thread is in?
You are asking for proof rather than the logic and reason behind the expansion of space.......
You really have to be kidding!
When you talk about space or spacetime and matter, you have to be referring to general relativity. General relativity is a extremely successful theory, describing the geometry and dynamics of objects in space/spacetime. Yes there are beginning to be some observations that do not quite fit, requiring the additions of dark mater and dark energy. That takes nothing away from the success of GR and it's improvement compared to Newtonian Dynamics which it replaced or superseded.
Generql Relativity has never even attempted to explain the mechanism of those interactions. It says space and matter interact dynamically and describes that interaction successfully. It says nothing about the mechanism(s) or why of those interactions.
I keep bring this up, but again there have been and are continuing attempts to come up with explanations of the mechanisms from the perspective of QM. There has been no entirely sucessful model/theory, that I am aware of.., yet.
Understanding that you are asking a question that you should know has no answer, makes the whole dialog seem to be at about the same level as a five year old who has just learned the word why.
Do your really think there is a scientific answer to your question?...., that remains consistent with the science folder this thread is in?
You are asking for proof rather than the logic and reason behind the expansion of space.......
You're ok, OnlyMe, and I know you mean well. However, you have just conflated universal expansion hypothesis/interpretations with GR theory of gravitation as it affects local matter moving through space and NOT with space as origin's statement re 'expanding space' implied without any explanation as to how that supposedly expanding space can carry galaxies with it.
GR is all about natural geodesics through space, not about space itself expanding in big bang hypothesis manner.
I would appreciate it if you kept your assumptions/conflations out of my exchange with origin, in the context wherein I just want his explanation/mechanism for his claim that 'expanding space' supposedly makes distant galaxies move with space in addition to their normal proper motion through space.
If neither he nor anyone else can do that, then his claim must fall under the category of inferred speculations and not fact. I've no objections to that. OK? Thanks.
So...
...origin, my last post/question to you remains to be answered in the context you claimed about expanding space and galaxy motion above that of proper motion. Thanks.
- Status
- Not open for further replies.
