Look at the image of the slinky that I posted, and you re-posted. Now read again the part where I say the weight has to be sufficient so the spring is within its linear region, i.e. obeys Hooke's Law, and how you can look at where this region starts by slowly adding weight (so accelerations are suppressed, so you stay linear physically and mathematically--no complex numbers aka "field extensions", no rotating vectors around a circle and so on).The God said:..so now you agree that spring extension will be non uniform with attached weight ?
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
A little math quiz
- Thread starter arfa brane
- Start date
Look at the image of the slinky that I posted, and you re-posted. Now read again the part where I say the weight has to be sufficient so the spring is within its linear region, i.e. obeys Hooke's Law, and how you can look at where this region starts by slowly adding weight (so accelerations are suppressed, so you stay linear physically and mathematically--no complex numbers aka "field extensions", no rotating vectors around a circle and so on).
Ok I looked at that.....
1. When there is no mass attached, extension is non uniform ie almost zero near the free end and some higher value near the hinged end...
2. Now we attach some mass (which should keep the spring in linear range), will the extension be uniform ?
If you say that yes, it will be uniform, then this mass has to compensate for the fixed non unifromity caused by spring self mass.....how is it possible for various masses within spring limits ?
Merely because it is assumed that the spring mass, per coil, is negligible compared to the attached mass subject to uniform gravitational acceleration..how is it possible for various masses within spring limits?
I think.
Ask a "real" physicist
But, you too can be a physicist! All for less than $10 a day!
1) acquire some springs. Springs come in many shapes and sizes. I would recommend not investigating the physics of vehicle suspension springs (but that's just me maybe), instead opting for those springs you can attach weights to that don't need to weigh tonnes.
2) investigate the linear responses of the springs to applied forces--you can use a set of say, kitchen weights, but you don't need to know what the mass of any weight is. Check out Hooke's Law.
3) upgrade to investigating the nonlinear responses of your springs to accelerations of the attached weights. No extra cost! (Gravity is free).
4) use a long, skinny type of spring and investigate what happens when you attach some weight, then twist the lower end of the spring around several times (i.e. apply torque), then let go. You should see standing waves as the system unwinds itself.
5) convince yourself that during oscillations with no initial twisting, the weight rotates around the axis of displacement, hence the spring rotates too. But the fixed end of the spring stays fixed, so this rotation isn't linear over the spring length.
6) convince yourself that even if the spring is not compressible, you can still calculate the force required to compress it to length zero.
7) ... etc.
1) acquire some springs. Springs come in many shapes and sizes. I would recommend not investigating the physics of vehicle suspension springs (but that's just me maybe), instead opting for those springs you can attach weights to that don't need to weigh tonnes.
2) investigate the linear responses of the springs to applied forces--you can use a set of say, kitchen weights, but you don't need to know what the mass of any weight is. Check out Hooke's Law.
3) upgrade to investigating the nonlinear responses of your springs to accelerations of the attached weights. No extra cost! (Gravity is free).
4) use a long, skinny type of spring and investigate what happens when you attach some weight, then twist the lower end of the spring around several times (i.e. apply torque), then let go. You should see standing waves as the system unwinds itself.
5) convince yourself that during oscillations with no initial twisting, the weight rotates around the axis of displacement, hence the spring rotates too. But the fixed end of the spring stays fixed, so this rotation isn't linear over the spring length.
6) convince yourself that even if the spring is not compressible, you can still calculate the force required to compress it to length zero.
7) ... etc.
Along with this statement: "tensors are linear maps from vectors to vectors", and rpenner's earlier post, plus some things someguy said, I get that the linear maps in the below text are those 2 x 2 real matrices acting on 2 x 1 vectors?
There is an analytic solution in $$\mathbb{R}^2$$
$$p = m \frac{d x}{d t}, F = \frac{d p}{d t}$$
$$F = -k x \Rightarrow \frac{d \quad }{d t} \begin{pmatrix} x \\ p \end{pmatrix} = \begin{pmatrix} 0 & m^{-1} \\ -k & 0 \end{pmatrix} \begin{pmatrix} x \\ p \end{pmatrix}$$
or this is simpler in coordinates of the same units:
$$\frac{d \quad}{d t} \begin{pmatrix} x \\ \frac{1}{\sqrt{k m}} p \end{pmatrix} = \begin{pmatrix} 0 & \sqrt{\frac{k}{m}} \\ - \sqrt{\frac{k}{m}} & 0 \end{pmatrix} \begin{pmatrix} x \\ \frac{1}{\sqrt{k m}} p \end{pmatrix}$$
or
$$\frac{d \quad }{d t} \begin{pmatrix} x \\ \frac{1}{\sqrt{k m}} p \end{pmatrix} = \sqrt{\frac{k}{m}} \begin{pmatrix} 0 & 1 \\ - 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ \frac{1}{\sqrt{k m}} p \end{pmatrix}$$
With solution
$$\begin{pmatrix} x(t) \\ \frac{1}{\sqrt{k m}} p(t) \end{pmatrix} = e^{ \sqrt{\frac{k}{m}} t \begin{pmatrix} 0 & 1 \\ - 1 & 0 \end{pmatrix} } \begin{pmatrix} x_0 \\ \frac{1}{\sqrt{k m}} p_0 \end{pmatrix}
= \begin{pmatrix} \cos \left( \sqrt{\frac{k}{m}} t \right) & \sin \left( \sqrt{\frac{k}{m}} t \right) \\ - \sin \left( \sqrt{\frac{k}{m}} t \right) & \cos \left( \sqrt{\frac{k}{m}} t \right) \end{pmatrix} \begin{pmatrix} x_0 \\ \frac{1}{\sqrt{k m}} p_0 \end{pmatrix}$$
or
$$ x(t) = \cos \left( \sqrt{\frac{k}{m}} t \right) x_0 + \frac{1}{\sqrt{k m}} \sin \left( \sqrt{\frac{k}{m}} t \right) p_0
\\ p(t) = - \sqrt{k m} \sin \left( \sqrt{\frac{k}{m}} t \right) x_0 + \cos \left( \sqrt{\frac{k}{m}} t \right) p_0 $$
So, just reviewing:
You have a spring at equilibrium with attached weight mg, and mg = kx. Now you can lift and drop the weight, or pull the weight down and let it go, thus using gravity or the spring force, to initiate SHM. Anyway, the weight oscillates up and down and this is mathematically equivalent to a particle in uniform circular motion around a circle whose diameter is twice the amplitude of the oscillations.
You have:

the diameter the spring oscillates along can be aligned with either the x or y axis, because it doesn't matter if $$ x(t) = A\, sin\, \omega t $$ or $$ y(t) = A\, sin\, \omega t $$ (where A = r).
So returning to the notation used by Wikipedia, and choosing y as the axis of motion, $$ y(t) = A\, sin\, \theta = A\, sin\,\omega t; Dy(t) = \omega A\, cos\, \omega t; D^2y(t) = -\omega^2A\, sin\, \omega t = -\omega^2y(t) $$.
$$ \Rightarrow D^2y = -\omega^2y \Rightarrow (D^2 + \omega^2)y = 0 $$
And because this means: $$ (D^2 + \omega^2)y = (D + i\omega)(D - i\omega)y = 0 $$, we can envisage the radius r = A as rotating around a circle with imaginary angular frequency $$ i\omega $$, the weight moving along y is a projection.
You have a spring at equilibrium with attached weight mg, and mg = kx. Now you can lift and drop the weight, or pull the weight down and let it go, thus using gravity or the spring force, to initiate SHM. Anyway, the weight oscillates up and down and this is mathematically equivalent to a particle in uniform circular motion around a circle whose diameter is twice the amplitude of the oscillations.
You have:
the diameter the spring oscillates along can be aligned with either the x or y axis, because it doesn't matter if $$ x(t) = A\, sin\, \omega t $$ or $$ y(t) = A\, sin\, \omega t $$ (where A = r).
So returning to the notation used by Wikipedia, and choosing y as the axis of motion, $$ y(t) = A\, sin\, \theta = A\, sin\,\omega t; Dy(t) = \omega A\, cos\, \omega t; D^2y(t) = -\omega^2A\, sin\, \omega t = -\omega^2y(t) $$.
$$ \Rightarrow D^2y = -\omega^2y \Rightarrow (D^2 + \omega^2)y = 0 $$
And because this means: $$ (D^2 + \omega^2)y = (D + i\omega)(D - i\omega)y = 0 $$, we can envisage the radius r = A as rotating around a circle with imaginary angular frequency $$ i\omega $$, the weight moving along y is a projection.
Last edited:
Although the wiki article on circular motion doesn't mention that SHM is defined on the real axis, it has this, (mentally replace R the radius with A the amplitude)
"
Circular motion can be described using complex numbers. Let the
 axis be the real axis and the
axis be the real axis and the
 axis be the imaginary axis. The position of the body can then be given as
axis be the imaginary axis. The position of the body can then be given as
 , a complex "vector":
, a complex "vector":
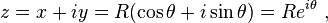
where
 is the imaginary unit, and
is the imaginary unit, and

is the angle of the complex vector with the real axis and is a function of time t. Since the radius is constant:
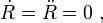
where a dot indicates time differentiation. With this notation the velocity becomes:

and the acceleration becomes:



The first term is opposite in direction to the displacement vector and the second is perpendicular to it"
The last sentence says acceleration is out of phase with the displacement vector by a factor of π, the second perpendicular term has the time derivative of $$ \omega $$ which only applies to non-uniform circular motion,
"
Circular motion can be described using complex numbers. Let the



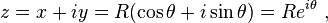
where


is the angle of the complex vector with the real axis and is a function of time t. Since the radius is constant:
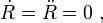
where a dot indicates time differentiation. With this notation the velocity becomes:

and the acceleration becomes:



The first term is opposite in direction to the displacement vector and the second is perpendicular to it"
The last sentence says acceleration is out of phase with the displacement vector by a factor of π, the second perpendicular term has the time derivative of $$ \omega $$ which only applies to non-uniform circular motion,
Last edited:
