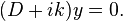No...
Take a spring of some mass...hang it vertically.....now the elongation on the turns closer to free side is almost nil, while much higher near the hinge ?
Now apply some mass....
A little math quiz
- Thread starter arfa brane
- Start date
No...
Take a spring of some mass...hang it vertically.....now the elongation on the turns closer to free side is almost nil, while much higher near the hinge ?
Now apply some mass....
Well, I must say this is one of the strangest threads to which I have ever contributed.
Like, the OP raises the perfectly reasonable question - given the isomorphism $$\mathbb{C} \simeq \mathbb{R}^2$$, why is the notation for their elements different.
We then move to tensor products, field extensions and some other bits of mathematics, through quantum interference, then to springs, accelerating or otherwise, and now we are here.
I am totally at a loss to see any connection between each of the OPer's successive posts.
It must be me........
Like, the OP raises the perfectly reasonable question - given the isomorphism $$\mathbb{C} \simeq \mathbb{R}^2$$, why is the notation for their elements different.
We then move to tensor products, field extensions and some other bits of mathematics, through quantum interference, then to springs, accelerating or otherwise, and now we are here.
I am totally at a loss to see any connection between each of the OPer's successive posts.
It must be me........
QH, What isomorphism $$\mathbb{C} \simeq \mathbb{R}^2$$? There is one of Abelian groups, none as rings or fields. One as real vector spaces, but none as real algebras or complex vector spaces or algebras. This lack of clarity underlies much confusion in this thread. The moment you say WHAT isomorphism, the answer becomes clear.
I think of this forum as "Physicists doing math badly." Helps me to make peace with what I read here. I'm as baffled as you as to what springs have to do with this question.
Last edited:
I'm not baffled at all. What springs "have to do with" the different (isomorphic?) spaces is obvious: springs are extended linearly under equilibrium and you can map this to $$ \mathbb R^2$$. But an oscillating spring maps to $$ \mathbb C $$.someguy said:
I don't know, perhaps it's a clue--oscillating or wavelike systems don't generally have maps to real vector spaces (?)
That isn't relevant to your claims about isomorphisms and algebras? As to the difference in notation, I think that's been answered several times.
So you keep "harping" on about this. Let's see if we can agree on this.......
$$\mathbb{R} \times \mathbb{R} \equiv \mathbb{R}^2$$ is not a field - there does not exist a multiplicative inverse for each element. However it is ring - there exists both additive and multiplicative identities and an inverse for addition.
Likewise, the field $$\mathbb{C}$$ is a ring, like any other field.
Both $$\mathbb{C}$$ and $$\mathbb{R}^2$$ can be viewed as Real modules (by virtue of the above). But, equally, both can be regarded as Real vector spaces (since $$\mathbb{R}$$ is a field).
So the isomorphism I claimed is a bijective ring homomorphism, a bijective R-module homomorphism, and also a bijective vector space homomorphism. But not a field homomorphism.
Except it seems the "real" physicists here are outnumbered. And, in terms of mathematics, the real guys at least know their calculus, and know it well.
It might look strange, but what I'm hoping is that some understanding of the differences between real and complex vector (and tensor) spaces will emerge.QuarkHead said:
Or perhaps I'll only manage to underline that physics is strictly an abuse of mathematics . . .
p.s. isn't it the case that a ring is, or has, an algebra defined on it? I thought that for instance, the real line with addition and multiplication is algebraic, or I thought that's what I was told. Should I think again?
It's necessary mathematical precision. If you tell me two things are isomorphic, I need to know what type of isomorphism. This entire thread is about the distinction between a real and a complex vector space, or between a vector space and an algebra. Precision is critical here. Not a point I can back down on, unfortunately; so if you still think I'm harping or being overly pedantic, perhaps we can drill down. Because I see this as the essence of the question.
Yes we are in total agreement on everything you wrote.
However, there's one more structure to consider. $$\mathbb{C}$$ is an $$\mathbb{R}$$-algebra and $$\mathbb{R}^2$$ is not.
An $$\mathbb{R}$$-algebra is a vector space over $$\mathbb{R}$$ that is also a ring, endowed with a multiplication that is compatible with scalar multiplication by reals. The complex numbers are an algebra over the reals. That's what makes them different than $$\mathbb{R}^2$$.
https://en.wikipedia.org/wiki/Algebra_over_a_field
To put this in perspective, the quaternions and octonions are also algebras over the reals. They're vector spaces plus a multiplication on the vectors that's compatible with multiplication by scalars.
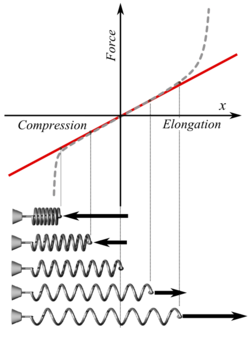
Your earlier remark about springs sounded interesting. Can you explain this in simple terms? You said a stationary spring was like $$\mathbb{R}^2$$ and an oscillating spring is like $$\mathbb{C}$$? Is it possible to put that in very simple terms? I looked up springs and evidently the force is kx where k is a constant. I can see how that's linear. That's literally everything I know about springs.
Even if it is, physical insight seems to have a lot to do with math. A lot of great mathematicians were physicists too.
A given ring could have a lot of algebras defined on it. A ring is an algebra over itself, after all.
You can think of an algebra as just one ring inside another. The reals inside the complex numbers for example. Any tme you have one ring inside another, the outer ring is a module over the inner one. (You need some regularity conditions such as that the rings both have 1 and that it's the same 1).
I think there's some confusion about the word algebraic versus "an" algebra. If you have a field inside another field (like the reals inside the complex numbers for example) a real number is algebraic over the rationals if it's the root of some polynomial having rational coefficients. So $$\sqrt{2}$$ is algebraic (being a root of the polynomial $$x^2 - 2)$$ and $$\pi$$ isn't (this requires proof, of course). That's a totally different meaning, in the context of determining whether polynomials have solutions that can be obtained via algebraic operations.
The complex numbers are "an algebra" over the reals because they're a vector space over the reals along with a multiplication that's compatible with scalar multiplication by reals. In that respect, the reals are trivially an algebra over themselves.
Can you explain that in simple terms?
Last edited:
someguy said:
Let D = d/dt, then a simple harmonic oscillator (no damping) is represented by: (for some constant k so we have $$ Dy = -ky $$)
Simple harmonic oscillator
The second order differential equation
which can be restated as
The expression in parenthesis can be factored out, yielding
which has a pair of linearly independent solutions:
The solutions are, respectively,
and
--https://en.wikipedia.org/wiki/Linear_differential_equation
The expression in parenthesis can be factored out, yielding
which has a pair of linearly independent solutions:
There's much for me to study here and I will look at that link and try to understand something about springs.
What I see here, from a purely algebraic point of view, is that you have a quadratic expression that is a sum of two squares, therefore it can not be factored any further over the field of real numbers. Just like $$x^2 + 1$$, which has no solution in the real numbers.
However if we are living in the complex numbers, then a sum of two squares factors. And in fact $$x^2 + 1$$ has a pair of solutions, $$i$$ and $$-i$$, and $$x^2 + 1$$ factors into monomials as $$(x+i)(x-i)$$.
So this actually another way of viewing the transition from the reals to the complex numbers. The complex numbers are algebraically closed and the reals aren't. Every polynomial with complex coefficients has a root in the complex numbers. Gauss proved that as his doctoral thesis in 1799, isn't that cool?
Anyway in your above derivation, you get to that step where you can't factor a quadratic over the reals so you just factor it over the complex numbers. That's a very pure-mathy kind of thing. I didn't need to understand any physics to see what they're doing. So there's a bridge between the math and the physics. I'm encouraged. I'll go take a look at the Wiki link. Spring theory not string theory!
Last edited:
Of course, the amplitude of an oscillating spring + weight is real, not complex. The domain of the solution space "has" to be the complex plane, as you say, there is no solution over the reals.
Physicists, of course, just choose whatever mathematics solves a problem. Perhaps I should have rewritten the above with a different notation for the constant k, so as not to confuse it with a spring constant. The perils of cut and paste math, I suppose.
ed: note that mg = kx, in vector form, is actually $$ m \vec g = k \vec x $$. The vector on the left is an acceleration vector and always points in the same direction. However, on the right the displacement vector can point anywhere (you can arrange the spring to be connected to a falling weight via a system of pulleys). Does that mean they must be independent vectors? That you can plot them on orthogonal axes in $$ \mathbb R^2 $$ might not be much of a proof.
Physicists, of course, just choose whatever mathematics solves a problem. Perhaps I should have rewritten the above with a different notation for the constant k, so as not to confuse it with a spring constant. The perils of cut and paste math, I suppose.
ed: note that mg = kx, in vector form, is actually $$ m \vec g = k \vec x $$. The vector on the left is an acceleration vector and always points in the same direction. However, on the right the displacement vector can point anywhere (you can arrange the spring to be connected to a falling weight via a system of pulleys). Does that mean they must be independent vectors? That you can plot them on orthogonal axes in $$ \mathbb R^2 $$ might not be much of a proof.
Last edited:
There is an analytic solution in $$\mathbb{R}^2$$
$$p = m \frac{d x}{d t}, F = \frac{d p}{d t}$$
$$F = -k x \Rightarrow \frac{d \quad }{d t} \begin{pmatrix} x \\ p \end{pmatrix} = \begin{pmatrix} 0 & m^{-1} \\ -k & 0 \end{pmatrix} \begin{pmatrix} x \\ p \end{pmatrix}$$
or this is simpler in coordinates of the same units:
$$\frac{d \quad}{d t} \begin{pmatrix} x \\ \frac{1}{\sqrt{k m}} p \end{pmatrix} = \begin{pmatrix} 0 & \sqrt{\frac{k}{m}} \\ - \sqrt{\frac{k}{m}} & 0 \end{pmatrix} \begin{pmatrix} x \\ \frac{1}{\sqrt{k m}} p \end{pmatrix}$$
or
$$\frac{d \quad }{d t} \begin{pmatrix} x \\ \frac{1}{\sqrt{k m}} p \end{pmatrix} = \sqrt{\frac{k}{m}} \begin{pmatrix} 0 & 1 \\ - 1 & 0 \end{pmatrix} \begin{pmatrix} x \\ \frac{1}{\sqrt{k m}} p \end{pmatrix}$$
With solution
$$\begin{pmatrix} x(t) \\ \frac{1}{\sqrt{k m}} p(t) \end{pmatrix} = e^{ \sqrt{\frac{k}{m}} t \begin{pmatrix} 0 & 1 \\ - 1 & 0 \end{pmatrix} } \begin{pmatrix} x_0 \\ \frac{1}{\sqrt{k m}} p_0 \end{pmatrix}
= \begin{pmatrix} \cos \left( \sqrt{\frac{k}{m}} t \right) & \sin \left( \sqrt{\frac{k}{m}} t \right) \\ - \sin \left( \sqrt{\frac{k}{m}} t \right) & \cos \left( \sqrt{\frac{k}{m}} t \right) \end{pmatrix} \begin{pmatrix} x_0 \\ \frac{1}{\sqrt{k m}} p_0 \end{pmatrix}$$
or
$$ x(t) = \cos \left( \sqrt{\frac{k}{m}} t \right) x_0 + \frac{1}{\sqrt{k m}} \sin \left( \sqrt{\frac{k}{m}} t \right) p_0
\\ p(t) = - \sqrt{k m} \sin \left( \sqrt{\frac{k}{m}} t \right) x_0 + \cos \left( \sqrt{\frac{k}{m}} t \right) p_0 $$
Last edited:
But isn't the solution a projection from a complex space onto a real one? I mean, $$ e^X = cos(X) + isin(X) = \begin{pmatrix} cos(X) & sin(X) \\ -sin(X) & cos(X) \end{pmatrix}$$. You have a complex number in your solution, represented as a real 2 x 2 matrix.
Last edited:
That's a way to look at it.
Another is from real analysis:
$$e^{\omega t { \tiny \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} } }
\\ = \sum \limits_{k=0}^{\infty} \frac{1}{k!} \left( \omega t \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right)^k
\\ = \sum \limits_{\ell=0}^{\infty} \left( \frac{1}{(4 \ell)!} \left( \omega t \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right)^{4\ell}
+ \frac{1}{(4 \ell +1)!} \left( \omega t \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right)^{4\ell+1}
+ \frac{1}{(4 \ell +2)!} \left( \omega t \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right)^{4\ell+2}
+ \frac{1}{(4 \ell +3)!} \left( \omega t \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right)^{4\ell+3} \right)
\\ = \sum \limits_{\ell=0}^{\infty} \left( \frac{(\omega t)^{4 \ell}}{(4 \ell)!} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}
+ \frac{(\omega t)^{4 \ell+1}}{(4 \ell +1)!} \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}
+ \frac{(\omega t)^{4 \ell+2}}{(4 \ell +2)!} \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}
+ \frac{(\omega t)^{4 \ell+3}}{(4 \ell +3)!} \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \right)
\\ = \sum \limits_{\ell=0}^{\infty} \begin{pmatrix} \frac{(\omega t)^{4 \ell}}{(4 \ell)!} - \frac{(\omega t)^{4 \ell+2}}{(4 \ell +2)!} & \frac{(\omega t)^{4 \ell+1}}{(4 \ell +1)!} - \frac{(\omega t)^{4 \ell+3}}{(4 \ell +3)!} \\ - \frac{(\omega t)^{4 \ell+1}}{(4 \ell +1)!} + \frac{(\omega t)^{4 \ell+3}}{(4 \ell +3)!} & \frac{(\omega t)^{4 \ell}}{(4 \ell)!} - \frac{(\omega t)^{4 \ell+2}}{(4 \ell +2)!} \end{pmatrix}
\\ = \begin{pmatrix} \sum \limits_{m=0}^{\infty} \frac{(-1)^m (\omega t)^{2m}}{(2m)!} & \sum \limits_{m=0}^{\infty} \frac{(-1)^m (\omega t)^{2m+1}}{(2m + 1)!} \\ \sum \limits_{m=0}^{\infty} - \frac{(-1)^m (\omega t)^{2m+1}}{(2m + 1)!} & \sum \limits_{m=0}^{\infty} \frac{(-1)^m (\omega t)^{2m}}{(2m)!} \end{pmatrix}
\\ = \begin{pmatrix} \cos \omega t & \sin \omega t \\ - \sin \omega t & \cos \omega t \end{pmatrix}$$
and
$$ \frac{d \quad}{d t} \begin{pmatrix} \cos \omega t & \sin \omega t \\ - \sin \omega t & \cos \omega t \end{pmatrix} = \omega \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} \cos \omega t & \sin \omega t \\ - \sin \omega t & \cos \omega t \end{pmatrix}$$
No complex numbers were harmed in the making of this post.
Another is from real analysis:
$$e^{\omega t { \tiny \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} } }
\\ = \sum \limits_{k=0}^{\infty} \frac{1}{k!} \left( \omega t \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right)^k
\\ = \sum \limits_{\ell=0}^{\infty} \left( \frac{1}{(4 \ell)!} \left( \omega t \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right)^{4\ell}
+ \frac{1}{(4 \ell +1)!} \left( \omega t \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right)^{4\ell+1}
+ \frac{1}{(4 \ell +2)!} \left( \omega t \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right)^{4\ell+2}
+ \frac{1}{(4 \ell +3)!} \left( \omega t \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right)^{4\ell+3} \right)
\\ = \sum \limits_{\ell=0}^{\infty} \left( \frac{(\omega t)^{4 \ell}}{(4 \ell)!} \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}
+ \frac{(\omega t)^{4 \ell+1}}{(4 \ell +1)!} \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}
+ \frac{(\omega t)^{4 \ell+2}}{(4 \ell +2)!} \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix}
+ \frac{(\omega t)^{4 \ell+3}}{(4 \ell +3)!} \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \right)
\\ = \sum \limits_{\ell=0}^{\infty} \begin{pmatrix} \frac{(\omega t)^{4 \ell}}{(4 \ell)!} - \frac{(\omega t)^{4 \ell+2}}{(4 \ell +2)!} & \frac{(\omega t)^{4 \ell+1}}{(4 \ell +1)!} - \frac{(\omega t)^{4 \ell+3}}{(4 \ell +3)!} \\ - \frac{(\omega t)^{4 \ell+1}}{(4 \ell +1)!} + \frac{(\omega t)^{4 \ell+3}}{(4 \ell +3)!} & \frac{(\omega t)^{4 \ell}}{(4 \ell)!} - \frac{(\omega t)^{4 \ell+2}}{(4 \ell +2)!} \end{pmatrix}
\\ = \begin{pmatrix} \sum \limits_{m=0}^{\infty} \frac{(-1)^m (\omega t)^{2m}}{(2m)!} & \sum \limits_{m=0}^{\infty} \frac{(-1)^m (\omega t)^{2m+1}}{(2m + 1)!} \\ \sum \limits_{m=0}^{\infty} - \frac{(-1)^m (\omega t)^{2m+1}}{(2m + 1)!} & \sum \limits_{m=0}^{\infty} \frac{(-1)^m (\omega t)^{2m}}{(2m)!} \end{pmatrix}
\\ = \begin{pmatrix} \cos \omega t & \sin \omega t \\ - \sin \omega t & \cos \omega t \end{pmatrix}$$
and
$$ \frac{d \quad}{d t} \begin{pmatrix} \cos \omega t & \sin \omega t \\ - \sin \omega t & \cos \omega t \end{pmatrix} = \omega \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} \cos \omega t & \sin \omega t \\ - \sin \omega t & \cos \omega t \end{pmatrix}$$
No complex numbers were harmed in the making of this post.
Last edited:
Ok. Well I consulted my old undergrad physics text, which has a whole chapter on oscillatory motion!
Here is a quote: ". . . when a particle moves with uniform circular motion, its projection on a diameter moves with SHM."
I've realised that an earlier post has an egregious error, in that case. If you have $$ D = \frac {d} {dt} $$, and $$ D^2y = -\lambda^2y $$, then $$ Dy \ne -\lambda y $$ (with different notation for the constant k). The sign in the right half of the last eqn is wrong, because the derivative of cos is -sin. All that is obvious from simple trigonometry.
That is you have the relation between period, angular frequency, and frequency: $$ \omega = \frac {2\pi} {P} = 2\pi \nu $$
And: $$ \frac {dx} {dt} = \omega A cos(\omega t + \alpha) \Rightarrow \frac {d^2x} {dt^2} = -\omega^2 A sin(\omega t + \alpha)$$
Here is a quote: ". . . when a particle moves with uniform circular motion, its projection on a diameter moves with SHM."
I've realised that an earlier post has an egregious error, in that case. If you have $$ D = \frac {d} {dt} $$, and $$ D^2y = -\lambda^2y $$, then $$ Dy \ne -\lambda y $$ (with different notation for the constant k). The sign in the right half of the last eqn is wrong, because the derivative of cos is -sin. All that is obvious from simple trigonometry.
That is you have the relation between period, angular frequency, and frequency: $$ \omega = \frac {2\pi} {P} = 2\pi \nu $$
And: $$ \frac {dx} {dt} = \omega A cos(\omega t + \alpha) \Rightarrow \frac {d^2x} {dt^2} = -\omega^2 A sin(\omega t + \alpha)$$
Last edited:
TG said:
An image of a slinky steel spring (or enough of the lower part), hanging vertically under its own weight. If you add a discrete weight (a discrete object with mass) by attaching it to the lower end, the spring should extend uniformly so there is an equal distance between windings. How big should the added weight be, though? What if it's less than the spring's mass?
p.s. Slinky turns 70 this year.
And, via a conspiracy of coincidence, that gives me pause to consider having a variable weight attached to the spring. A container of some kind, maybe a bowl you can trickle sand, water, oil, ..., into. If the rate of change in mass is kept constant, you must have dm/dt = constant, when you stop adding mass you're just weighing that mass with the spring and everything is linear.
If dm/dt is not constant you will accelerate the bowl and 'the system' will oscillate.
In SHM, there are three components to the motion: displacement, velocity, and acceleration. Velocity is 90° out of phase with displacement and acceleration, which are 180° out of phase.
You can represent all three components of motion as rotating vectors in a real vector space, but they're just as as happy in a complex vector space.
If dm/dt is not constant you will accelerate the bowl and 'the system' will oscillate.
In SHM, there are three components to the motion: displacement, velocity, and acceleration. Velocity is 90° out of phase with displacement and acceleration, which are 180° out of phase.
You can represent all three components of motion as rotating vectors in a real vector space, but they're just as as happy in a complex vector space.
Last edited:
So I think it's about degrees of freedom in both mathematical and physical domains. The above thought experiment with changing mass is equivalent to having a constant mass, i.e. dm/dt = 0 = constant and a constant velocity during the displacement. Acceleration is a degree of freedom, and it's suppressed.
You can suppress acceleration of a fixed weight by lowering it by hand, effectively generating a 'function of velocity' that suppresses the force of gravity, a coefficient of viscosity in other words that has a force component with units: velocity x Newton-seconds per metre. The weight should separate from your hand and maintain an equilibrium position as you lower it.
It's totally analogous to viscosity, because it mimics a mass in free fall in a viscous fluid which has reached terminal velocity.
You can suppress acceleration of a fixed weight by lowering it by hand, effectively generating a 'function of velocity' that suppresses the force of gravity, a coefficient of viscosity in other words that has a force component with units: velocity x Newton-seconds per metre. The weight should separate from your hand and maintain an equilibrium position as you lower it.
It's totally analogous to viscosity, because it mimics a mass in free fall in a viscous fluid which has reached terminal velocity.
An image of a slinky steel spring (or enough of the lower part), hanging vertically under its own weight. If you add a discrete weight (a discrete object with mass) by attaching it to the lower end, the spring should extend uniformly so there is an equal distance between windings. How big should the added weight be, though? What if it's less than the spring's mass?
p.s. Slinky turns 70 this year.
So, the spring has non uniform extension due to its weight, but as soon as we hang a discrete mass to it, the extension becomes uniform......If this is true, we will find out......then its great, but surprising part is that this discrete mass has to extend the (near to free end) turns more and near to hinged turn less, to make a non uniform extension uniform and that too by same amount irrespective of value of discrete mass (within spring limits). But nonethless the extension solely by this mass is not uniform, only a non uniform extension can make a non uniform (unattached extension) uniform.
Not necessarily, the spring needs to be within its range of linearity. If the discrete mass is too large it will overextend the spring (more or less irreversible), if its too small, it will underextend it. It will be still mostly weighing itself and look like the slinky image.The God said:
Suppose you can hang a bowl at the bottom of a spring and this bowl weighs much less than the spring itself. You can investigate where the spring begins to exhibit linear behaviour by slowly adding mass to the bowl.
Often, the nonlinear regions of an otherwise linear system are more interesting, sometimes there is chaotic behaviour in these regions (this is more true for electronic devices with resistance, capacitance, and inductance, for instance).
So we need to take notice, as it were, of Hooke's Law:
Not necessarily, the spring needs to be within its range of linearity. If the discrete mass is too large it will overextend the spring (more or less irreversible), if its too small, it will underextend it. It will be still mostly weighing itself and look like the slinky image.
Suppose you can hang a bowl at the bottom of a spring and this bowl weighs much less than the spring itself. You can investigate where the spring begins to exhibit linear behaviour by slowly adding mass to the bowl.
Often, the nonlinear regions of an otherwise linear system are more interesting, sometimes there is chaotic behaviour in these regions (this is more true for electronic devices with resistance, capacitance, and inductance, for instance).
So we need to take notice, as it were, of Hooke's Law:
I have said within spring limits...so now you agree that spring extension will be non uniform with attached weight ?