A little math quiz
- Thread starter arfa brane
- Start date
Actually, it's obvious that any ordered tuple is a list of orthogonal elements, whatever the elements are. The order imposes a canonical basis, moreover a list is a recursive object.
And I think also I've managed to work something out about degrees of freedom related to complex dimensions.
In circuit analysis, you have Fourier transforms of some input waveform, a network of active and passive circuit elements with an overall response which is complex. The real and imaginary parts of this response have a physical existence in the frequency domain.
Note an input waveform is defined as a time-varying voltage (electric potential), as is the output waveform, but both could be defined in terms of time-varying magnetic potential.
However, that particular degree of freedom hasn't been exploited much and the convention is to measure the electric field (viz voltmeters, oscilloscopes),
A waveform is a physical object that is described by complex numbers, but you need to use just one complex dimension for classical waves. Why, is because voltage and current rotating vectors can also change in magnitude--the extra degree of freedom.
In quantum mechanics where the vector space is $$ \mathbb C^2 $$, one degree of freedom is lost with the restriction that the probabilities of measurement outcomes sum to 1.
A photon is spin 1, so it can have parallel, antiparallel, or transverse spin (polarization), but the latter mode is a "lost" degree of freedom because any measurement must occur at the speed of light (but, hang on, why is that a problem?).
And I think also I've managed to work something out about degrees of freedom related to complex dimensions.
In circuit analysis, you have Fourier transforms of some input waveform, a network of active and passive circuit elements with an overall response which is complex. The real and imaginary parts of this response have a physical existence in the frequency domain.
Note an input waveform is defined as a time-varying voltage (electric potential), as is the output waveform, but both could be defined in terms of time-varying magnetic potential.
However, that particular degree of freedom hasn't been exploited much and the convention is to measure the electric field (viz voltmeters, oscilloscopes),
A waveform is a physical object that is described by complex numbers, but you need to use just one complex dimension for classical waves. Why, is because voltage and current rotating vectors can also change in magnitude--the extra degree of freedom.
In quantum mechanics where the vector space is $$ \mathbb C^2 $$, one degree of freedom is lost with the restriction that the probabilities of measurement outcomes sum to 1.
A photon is spin 1, so it can have parallel, antiparallel, or transverse spin (polarization), but the latter mode is a "lost" degree of freedom because any measurement must occur at the speed of light (but, hang on, why is that a problem?).
Last edited:
That's why some references emphasize that it's not a normal vector space, but a projective one and a wave function is a ray in this projective space.
Thus $$15 \left| \psi \right> = \left| \psi \right>$$ and $$ \left< \psi_i | \psi_i \right> = 1, \; \left< \psi_i | \psi \right> \neq 0 \Rightarrow \left| \psi_i \right> = \left| \psi_i \right> \left< \psi_i | \psi \right>$$
which makes no sense for an ordinary vector space.
In fact you have $$ e^{i\phi} |\psi \rangle = |\psi \rangle $$.
And you have the Bloch sphere.
What about motion, though? Particles like electrons in a beam all have the same forward velocity, and the spin vector can point in this direction or away from it. Does motion imply another constraint on degrees of freedom (in the state space)?
And you have the Bloch sphere.
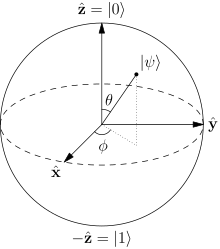
Bloch sphere representation of a qubit. The probability amplitudes in the text are given byand
.
What about motion, though? Particles like electrons in a beam all have the same forward velocity, and the spin vector can point in this direction or away from it. Does motion imply another constraint on degrees of freedom (in the state space)?
Last edited:
Here's some wikipedia stuff that I can make some sense of, which might be germane to QuarkHead's posts
So, a complex number is an extension of scalars . . .? Or what mathematicians call a field extension?
And
Let V be a real vector space. The complexification of V is defined by taking the tensor product of V with the complex numbers (thought of as a two-dimensional vector space over the reals):
The subscript R on the tensor product indicates that the tensor product is taken over the real numbers (since V is a real vector space this is the only sensible option anyway, so the subscript can safely be omitted). As it stands, VC is only a real vector space. However, we can make VC into a complex vector space by defining complex multiplication as follows:
More generally, complexification is an example of extension of scalars – here extending scalars from the real numbers to the complex numbers – which can be done for any field extension, or indeed for any morphism of rings.
So, a complex number is an extension of scalars . . .? Or what mathematicians call a field extension?
By the nature of the tensor product, every vector v in VC can be written uniquely in the form
where v1 and v2 are vectors in V. It is a common practice to drop the tensor product symbol and just write
Multiplication by the complex number a + ib is then given by the usual rule
We can then regard VC as the direct sum of two copies of V:
with the above rule for multiplication by complex numbers.
And
Dual spaces and tensor products
The dual of a real vector space V is the space V* of all real linear maps from V to R. The complexification of V* can naturally be thought of as the space of all real linear maps from V to C (denoted HomR(V,C)). That is,
The isomorphism is given by
where φ1 and φ2 are elements of V*. Complex conjugation is then given by the usual operation
Given a real linear map φ : V → C we may extend by linearity to obtain a complex linear map φ : VC → C. That is,
This extension gives an isomorphism from HomR(V,C)) to HomC(VC,C). The latter is just the complex dual space to VC, so we have a natural isomorphism:
More generally, given real vector spaces V and W there is a natural isomorphism
Complexification also commutes with the operations of taking tensor products, exterior powers and symmetric powers. For example, if V and W are real vector spaces there is a natural isomorphism
Note the left-hand tensor product is taken over the reals while the right-hand one is taken over the complexes. The same pattern is true in general. For instance, one has
In all cases, the isomorphisms are the “obvious” ones.
Last edited:
The God said: "A complex number in complex plane is certainly a vector"
But it has been explained that the field $$\mathbb{C}$$ can legitimately be regarded as a vector space over itself. Unless you wish to assert otherwise, or that elements in a vector space are not vectors, you are quite mistaken.
So, measurement and the motion of particles, it seems, are strongly connected. Give an electron a classical velocity along the x axis so then you are free to choose two other axes to do--what? Given a velocity and an axis, it seems time is no longer a free choice either (history aside) for one dimension of space.
OK.
You're now free to choose a measurement basis; an electron passing through a non-linear magnetic field as in a Stern-Gerlach apparatus, will emerge at an angle that depends on its spin and on its path through the field (the beam spreads into a shape like the outline of a lozenge, in reality).
The freedom to choose a basis lies around the axis of motion of the beam, and there are two dimensions left, since the first has been chosen. Actually, two dimensions are chosen when an electron has a velocity, one is the time dimension. Time appears to have a special kind of functionality, in that it becomes redundant in a somewhat mystifying way.
I can illustrate that particular quantum mysticism with the standard double slit diffraction of electrons. With a beam of millions of electrons you get an interference pattern that suggests each electron is part of the same field (of "matter waves"), i.e. there is some kind of standing wave each electron stays coherent with, before and after the slits, and this must have the structure of a classical wave, otherwise there would be no region where the waves interfere, and no pattern.
Moving the screen slightly doesn't change the pattern, the screen does have to be a classical distance from the two slits and the region of interference though. And the clincher is that single electrons (i.e. one at a time) will produce a pattern, as if each particle remains coherent with the same classical waveform with its fixed region of interference (but where is it?). Time is linear (because you add all the times for each electron together), but redundant (the time values you add up have no effect on any outcome).
Weird huh?
Last edited:
A short proof that, indeed $$ e^{i\phi} |\psi \rangle = |\psi \rangle $$.
So the inner product is
The factor $$ e^{i\phi} $$ is called the global phase, and is redundant.
The reason I write it once in $$ \langle\psi| e^{i\phi}|\psi \rangle $$ is that:
The notation is for the inner product, if this is for $$ e^{i\phi}|\psi \rangle $$ with itself, the row vector must have the inverse factor $$ e^{-i\phi} $$, because it's the conjugate transpose.
The probability amplitudes have to have inverses--the probability of spin up is the inverse of the probability of spin down.
Who knows? But it keeps everything in a unit probability space.
$$ e^{i\phi} |\psi \rangle = e^{i\phi}\alpha |0\rangle + e^{i\phi}\beta |1\rangle $$, and
$$ \langle\psi | = \overline \alpha \langle 0 | + \overline \beta \langle 1| $$
$$ \langle\psi | = \overline \alpha \langle 0 | + \overline \beta \langle 1| $$
So the inner product is
$$ \langle\psi |\psi \rangle = (\overline \alpha \langle 0 | + \overline \beta \langle 1|)(\alpha |0\rangle + \beta |1\rangle) = \overline \alpha \alpha +\overline \beta \beta = |\alpha|^2 + |\beta|^2 $$.
And, $$ \langle\psi| e^{i\phi}|\psi \rangle = (\overline \alpha e^{-i\phi}\langle 0 | + \overline \beta e^{-i\phi}\langle 1|)(\alpha e^{i\phi} |0\rangle + \beta e^{i\phi}|1\rangle) = \overline \alpha \alpha +\overline \beta \beta = |\alpha|^2 + |\beta|^2 $$.
The factor $$ e^{i\phi} $$ is called the global phase, and is redundant.
The reason I write it once in $$ \langle\psi| e^{i\phi}|\psi \rangle $$ is that:
The notation is for the inner product, if this is for $$ e^{i\phi}|\psi \rangle $$ with itself, the row vector must have the inverse factor $$ e^{-i\phi} $$, because it's the conjugate transpose.
The probability amplitudes have to have inverses--the probability of spin up is the inverse of the probability of spin down.
Who knows? But it keeps everything in a unit probability space.
Last edited:
As far as I know, it doesn't have anything to do with measurement. Rather, the third polarization option is usually lost because it requires the field to oscillate along the axis of propagation, which does not happen in free space. One of my coworkers works with optical fibers, in which the speed of light is slowed significantly; in this situation, light can propagate in "somersault" modes with nonzero polarization along all three axes.
, yes, thanks. I can recall reading about polarization modes like that a few years ago. So it isn't a problem except for free photons, when it is a problem?Fedni48 said:
Except for the speed of light having something to do with measurement of light? The electric field is oscillating along the axis of motion, meaning it is moving faster than the speed of light in that medium. In a vacuum SR says it can't.
Last edited:
On the topic of electron interference: the interference pattern is a feature of particles and beams of particles in general, it seems to be a quantum mechanical phenomenon that does not depend on charge or spin, or mass, and it doesn't depend on time either. But, the electron matter field as some kind of standing wave idea must have wavefronts (of whatever the standing wave is) moving towards the screen.
So assume each electron has the same wavelength as it reaches the double slit, and two interfering wave sources aka ripples in the field leave the slits with the same wavelength, and assume what interferes isn't waves of material stuff, but probabilities as complex amplitudes, and there we go.
So assume each electron has the same wavelength as it reaches the double slit, and two interfering wave sources aka ripples in the field leave the slits with the same wavelength, and assume what interferes isn't waves of material stuff, but probabilities as complex amplitudes, and there we go.
Well, be careful here - a complex number is also a scalar!
Here's some easy mathematics you won't really want.....
A number - a scalar - is said to algebraic if it the solution to a polynomial with rational coefficients: that's a definition. Consider the simplest example $$x^2+1=0$$ has no Real solution. One says that $$\mathbb{R}$$ is algebraically incomplete. We can "complete" the Reals by adjoining the imaginary unit $$i,\,\,i^2=-1$$ and say that $$R(i)$$ is the algebraic completion of the Reals.
But since every $$z \in \mathbb{C}$$ can be written as $$z=x+yi,\,\,x,y \in \mathbb{R}$$ one can equate $$R(i) \equiv \mathbb{C}$$, and say that $$\mathbb{C}$$ is a field extension for $$\mathbb{R}$$. One writes $$\mathbb{R}:\mathbb{C}$$ for this.
Field extensions are important in Galois Theory, which is not the subject of this thread - sorry
After this (probably unwelcome) interjection, you can get on with your physics
/slaps_forehead Of course! every $$ x \in \mathbb R$$ can be written as $$ x = a + b,\,a,b \in \mathbb R$$.
My understanding of Galois Theory is that it currently has a lot to do with encoding.
As to completion: $$ \mathbb C^2 $$ is called a complete vector space (a Hilbert space), how is it 'completed'.
I was really just interested in I guess any relations that might stand out between complex spaces of low dimension. An interesting detail is the unitarity condition in $$ \mathbb C^2 $$ : $$ |\alpha|^2 + |\beta|^2 = 1 $$ reducing the four dimensions to three. I think it says the fourth dimension is a unit of probability (whatever that might mean). Anyway, the condition is something imposed on the Hilbert space, it doesn't seem to be connected to completion.
But suppose you think you could try $$ \mathbb C^3 $$? Why wouldn't it describe qubits or some qubit state? What does it look like anyway?
I'm still not sure why my tensor product should be $$ w \otimes \overline z $$, I'm leaning towards something about dual spaces but I can't make out what it says yet.
Last edited:
Why the dual slit experiment isn't BS:
Thomas Young sketched a region of interference of dual waves when he did his double slit experiment with sunlight.
What was he trying to think about?
What I'm saying is that electron double slit interference has the same kind of 'standing' wave pattern but of probability amplitudes. A probability wave field perhaps. This field does exist, but only when an electron or a beam of electrons propagates through the slits. Since the electrons can be single particles, obviously coherence of the beam itself has no effect--each electron sees the same field (analogously, the field of ripple-waves remains stable as long as wavelengths stay constant over time). The only important parameter is wavelength, and each electron has the same wavelength (velocity).
The rays in the diagram above are where the ripples interfere destructively, and the wave (or wavelet) trains between these rays are those parts of the overall field (of ripple-waves) that reach a screen.
Analogously, each electron randomly chooses a wave train as it propagates through the field, but this field is 'made out of' probability amplitudes.
Thomas Young sketched a region of interference of dual waves when he did his double slit experiment with sunlight.
What was he trying to think about?
What I'm saying is that electron double slit interference has the same kind of 'standing' wave pattern but of probability amplitudes. A probability wave field perhaps. This field does exist, but only when an electron or a beam of electrons propagates through the slits. Since the electrons can be single particles, obviously coherence of the beam itself has no effect--each electron sees the same field (analogously, the field of ripple-waves remains stable as long as wavelengths stay constant over time). The only important parameter is wavelength, and each electron has the same wavelength (velocity).
The rays in the diagram above are where the ripples interfere destructively, and the wave (or wavelet) trains between these rays are those parts of the overall field (of ripple-waves) that reach a screen.
Analogously, each electron randomly chooses a wave train as it propagates through the field, but this field is 'made out of' probability amplitudes.
Ok, a little aside on the topic of measurement. This appears to require the existence of real space and time, because ultimately those are the only things we can measure.
But, you need energy too, because without motion, measurement is unphysical, say.
Look again at currents and voltages, these along with frequency are sufficient to describe (with "reasonable" accuracy) the response of any network of resistors, capacitors, and inductors, given some input, and such networks are easily extended to include active elements like transistors, op-amps etc. But a Volt has physical units of Newtons per Coulomb.
I think this is a little unsatisfactory. Newtons have units of mass times acceleration, what's mass doing in there? When you measure a voltage, the measurement has nothing to do with kilograms, so what the hell?
Ok, you can say there isn't a problem, it's just an accident of history, a force is a force whether it's pushing or pulling some mass, or pushing or pulling some charge. But, daing, can't I convert it into something that doesn't include mass units?
Why is it not a problem?
ed: sorry, mistake. A Volt has units Newton-metres per Coulomb.
But, you need energy too, because without motion, measurement is unphysical, say.
Look again at currents and voltages, these along with frequency are sufficient to describe (with "reasonable" accuracy) the response of any network of resistors, capacitors, and inductors, given some input, and such networks are easily extended to include active elements like transistors, op-amps etc. But a Volt has physical units of Newtons per Coulomb.
I think this is a little unsatisfactory. Newtons have units of mass times acceleration, what's mass doing in there? When you measure a voltage, the measurement has nothing to do with kilograms, so what the hell?
Ok, you can say there isn't a problem, it's just an accident of history, a force is a force whether it's pushing or pulling some mass, or pushing or pulling some charge. But, daing, can't I convert it into something that doesn't include mass units?
Why is it not a problem?
ed: sorry, mistake. A Volt has units Newton-metres per Coulomb.
Last edited:
Yeah, physics is about measurement, and measurement is about units of space and time. What about kilograms and coulombs? It turns out you measure these by measuring . . . space and time, and in the end, physics is also about multiplying units together, or using units and 'inverse' units, for example $$ s^{-1} $$ for frequency.
There are physical constants we can measure (we don't know what they are unless we measure them), like Newton's gravitational constant. Being a constant, maybe it's ok to multiply whatever you want that has units of mass in it, maybe not. In other words, if you multiply volts by G, to factor out the mass units, what changes? You of course need to deal with V = IR.
Ok, V = IR has nothing to do with gravity, you say. No, it doesn't, but multiplication of both sides of an equation by a constant is mathematically allowed. Or I could say, I'm just using a natural constant with the right units, to see if it introduces any problems.
Sometimes, maybe it helps to be anecdotal. Suppose you're enrolled in a physics course and you have some experiments to do. You have access to all the equipment you need to do each experiment, but you have to work out how to set it up yourself (it's one of those tough-love physics courses). What you are told is what you're supposed to measure, take photos of, calculate from information you collect, etc.
Ok, so one of the experiments is to determine the spring constants of a set of springs, using a set of unmarked weights of different mass. You are given a metre ruler which is marked and aligned in a frame you can hang the springs on. So you have one standard unit of distance, but no unit of mass. You will have to determine the spring constants against a unit of mass that you yourself choose, i.e. one of the unmarked weights. The experiment is do-able.
But, what's the significance?
There are physical constants we can measure (we don't know what they are unless we measure them), like Newton's gravitational constant. Being a constant, maybe it's ok to multiply whatever you want that has units of mass in it, maybe not. In other words, if you multiply volts by G, to factor out the mass units, what changes? You of course need to deal with V = IR.
Ok, V = IR has nothing to do with gravity, you say. No, it doesn't, but multiplication of both sides of an equation by a constant is mathematically allowed. Or I could say, I'm just using a natural constant with the right units, to see if it introduces any problems.
Sometimes, maybe it helps to be anecdotal. Suppose you're enrolled in a physics course and you have some experiments to do. You have access to all the equipment you need to do each experiment, but you have to work out how to set it up yourself (it's one of those tough-love physics courses). What you are told is what you're supposed to measure, take photos of, calculate from information you collect, etc.
Ok, so one of the experiments is to determine the spring constants of a set of springs, using a set of unmarked weights of different mass. You are given a metre ruler which is marked and aligned in a frame you can hang the springs on. So you have one standard unit of distance, but no unit of mass. You will have to determine the spring constants against a unit of mass that you yourself choose, i.e. one of the unmarked weights. The experiment is do-able.
But, what's the significance?
Last edited:
Using matrix notation, the inner product is $$ A^{\dagger} B = \begin{pmatrix} \bar{a}_1 & \bar{a}_2 & \bar{a}_3 & \dots & \bar{a}_n \end{pmatrix} \begin{pmatrix} b_1 \\ b_2 \\ b_3 \\ \vdots \\ b_n \end{pmatrix} $$ such that $$A^{\dagger} A$$ is a non-negative real number.
Thus $$\frac{B^{\dagger} A}{B^{\dagger} B} B$$ (for a real or complex vector) the component of A which points in the direction of B. But that's a linear map -- a projection operation with only one non-zero eigenvalue of 1. We can write that operator as $$P_B = \frac{B B^{\dagger} }{B^{\dagger} B}$$.
Thus $$P_B B = B$$, and $$P_B P_B A = P_B A = \frac{B^{\dagger} A}{B^{\dagger} B} B$$ and $$B^{\dagger} ( I - P_B ) A = 0 $$.
I confess I remain confused about $$ \mathbb C \otimes \mathbb C $$.
In $$ \mathbb C^2 $$ inner products and tensor products describe entirely different objects.
In $$ \mathbb C^2 $$ inner products and tensor products describe entirely different objects.